(преведено от гръцки. кръгъл) – плоска трансцендентална крива, която се описва от точка върху окръжност с радиус rтъркаляне по права линия без плъзгане (трансцендентална крива е крива, която не може да бъде описана с алгебрично уравнение в правоъгълни координати). Неговото параметрично уравнение

х = rt – r грях t,
г= r – r cos t

Точките на пресичане на циклоидата с правата линия, по която окръжността се търкаля (тази окръжност се нарича генерираща окръжност, а правата, по която се търкаля, се нарича директива) се наричат ​​точки на върховете, а най-високите точки на циклоидата , разположени в средата между съседни върхови точки, се наричат ​​върхове на циклоидата.

Галилео Галилей е първият, който изучава циклоида. Дължината на една циклоидна арка е определена през 1658 г. от английския архитект и математик Кристофър Рен, автор на проекта и строител на купола на катедралата Сейнт Пол в Лондон. Оказа се, че дължината на циклоидата е равна на 8 радиуса на образуващата окръжност.
Едно от забележителните свойства на циклоида, което му е дало името - брахистохрон (от гръцките думи "най-кратък" и "време") е свързано с решаването на проблема за най-стръмното спускане. Възникна въпросът каква форма трябва да се придаде на добре полиран (за почти премахване на триенето) жлеб, свързващ две точки, така че топката да се търкаля от една точка в друга за възможно най-кратко време. Братята Бернули доказват, че изкопът трябва да има формата на низходящ циклоид.

Кривите, свързани с циклоидата, могат да бъдат получени чрез разглеждане на траекториите на точки, които не са разположени върху генериращата окръжност.

Нека точката От 0е вътре в кръга. Ако се пренесе От 0спомагателна окръжност със същия център като генериращата окръжност, тогава, когато генериращата окръжност се търкаля по права линия ABмалък кръг ще се търкаля в права линия А´ IN´, но търкалянето му ще бъде придружено от плъзгане и точка От 0описва крива, наречена съкратена циклоида.

По подобен начин се дефинира удължена циклоида - това е траекторията на точка, разположена върху продължение на радиуса на образуващата окръжност, докато търкалянето е придружено от плъзгане в обратна посока.

Циклоидните криви се използват в много технически изчисления и техните свойства се използват, например, при конструиране на профили на зъбни колела, в циклоидни махала, в оптиката и по този начин изследването на тези криви е важно от приложна гледна точка. Също толкова важно е, че, изучавайки тези криви и техните свойства, учените от 17 век. разработи техники, които доведоха до създаването на диференциално и интегрално смятане, а брахистохронният проблем беше стъпка към изобретяването на вариационното смятане.

Елена Малишевская

Спомнете си тези оранжеви пластмасови ka-ta-fo-you - светлина-от-ra-zha-te-li, прикрепени-la-yu-schi-e-sya към спиците на ve-lo-si-ped-no- отивам ко-ле-са? Прикрепете ka-ta-fot към самия ръб на ko-le-sa и следвайте неговия tra-ek-to-ri-ey. Получените криви са в горната част на семейството циклоиди.

В същото време co-le-so се нарича про-от-кръг (или кръг) на cycl-o-i-dy.

Но да се върнем в нашия век и да преминем към по-модерни технологии. По пътя падна ка-му-шек, който се заби в потока на ко-ле-са. След като завъртите няколко кръга с колелото, къде отива камъкът, когато изскочите от потока? Срещу дясното движение на мотоциклета или по протежение на дясната страна?

Както знаете, свободното движение на тялото е по пътя по пътя към тази траектория, по която след това се е движил. Ka-sa-tel-naya към cycl-o-i-de винаги е вдясно по посока на движението и минава през горната точка ku около околността. Според дясната посока на движение, нашият ka-mu-shek също се движи.

Помните ли как карахте през локвите в детството си на велосипед без задно крило? Мократа ивица по гърба ви е потвърждението на очакванията на живота, че току-що е получил ре-зул -та-та.

17 век е векът на цикъла. Най-добрите учени са изследвали удивителните му свойства.

Някакъв вид tra-ec-to-ria ще пренесе тялото, движещо се под действието на силата на гравитацията, от една точка до друга за кратко време? Това беше една от първите задачи на този na-u-ki, който сега се използва като va-ri-a-tsi-on-noe.

Ми-ни-ми-зи-ро-ват (или макс-си-ми-зи-ро-ват) можете да имате различни неща - дължина на пътя, скорост, време. В za-da-che за bra-hi-sto-khron mi-ni-mi-zi-ru-et-sya е време (какво по дяволите-ki-va-et-sya sa-mime на -name: гръцки βράχιστος - най-малко, χρόνος - време).

Първото нещо, което идва на ум, е права линия tra-ek-to-ria. Да, ще разгледаме и цикъла на връщане с точката на връщане в горната част на дадените точки. И, следвайки Ga-li-leo Ga-li-le-em, - четвърт вертикален кръг, който свързва нашите точки.

Защо Ga-li-leo Ga-li-lei погледна четвърт вертикалния кръг и реши, че това е най-доброто в смисъл le time-me-ni tra-ek-to-ria спускане? Той написа повредени в него и забеляза, че с увеличаването на броя на връзките, времето по-късно намалява. Оттук Га-ли-лей естествено се премести в кръга, но направи грешния извод, че тази тра-ек -рия е най-добрата от всички възможни. Както виждаме, най-добрият tra-ek-to-ri-ey е cycl-o-i-da.

Чрез две дадени точки е възможно да се създаде единичен цикъл при условие, че в горната точка има точка на връщане на цикъла. И дори когато цикълът дойде под копелето, за да премине през втората точка, той пак ще вие ​​от най-бързото спускане!

Друга красива za-da-cha, свързана с cycl-lo-i-da, - za-da-cha за ta-u-to-chron. В превод от гръцки ταύτίς означава „същият“, χρόνος, както вече знаем, „време“.

Ще направим три хълма един по един с про-фи-лем под формата на цикли, така че краищата на хълмовете да са подравнени и да са разположени в горната част на цикъла. Настроихме три bo-bah за различни you-so-yous и нека да продължим. Изненадващ факт е, че всеки ще слезе един ден!

През зимата можете да построите пързалка от лед в двора си и да проверите този имот на живо.

For-yes-cha-about-that-chrono-it-in-the-look-up-of-such-a-curve that, starting from any-bo-go-start- Но в крайна сметка, времето на спускането до дадената точка ще бъде същото.

Christian Huy-gens знае, че единственото нещо, което е хронично, е cycl-o-i-da.

Разбира се, Guy-gen-sa не ин-t-re-so-val спускането по ледените планини. По това време учените не са имали толкова голяма работа от любов към изкуството. За-да-че-сме-изучени-е-хо-ди-от живота и за-про-с от онези времена. През 17 век морските пътувания на дълги разстояния вече са завършени. Shi-ro-tu sea-rya-ki вече са успели да определят точно до сто, но е изненадващо, че дълго време не могат да определят - да се справят с всичко. И един от методите преди la-gav-shih от shi-ro-you се основаваше на наличието на точен chro-no-met ров

Първият, който се сети да направи ma-yat-no-нови часовници, които биха били точни, беше Ga-li-leo Ga-li-ley. Но в момента, в който започва да ги пресъздава, той вече е стар, ослепял е и в оставащата година ученият няма време да завърши живота си. Той казва това на сина си, но той се колебае и започва да е--------------------------- близо до смъртта и няма време да седне надолу. Следващата известна фигура е Кристиан Хюйгенс.

Той забеляза, че периодът на ko-le-ba-niya обикновено ma-yat-ni-ka, ras-smat-ri-vav-she-go-sya Ga-li- le-em, za-vis-sit from- от-началото-на-ло-же-ния, т.е. от am-pl-tu-dy. Мислейки каква трябва да бъде траекторията на движение на товара, така че времето да не зависи от него -se-lo от am-pl-tu-dy, той решава за-da-chu за това-u-to-chron. Но как можете да накарате товара да се движи по цикличен начин? Превод на theo-re-ti-che-re-studies в практически-ti-che-равнина, Guy-gens de-la-et "бузи", на които on-ma-you-va-et-sya ve- rev-ka ma-yat-no-ka, и решава още няколко ma-te-ma-ti-che -skih задачи. Той твърди, че „бузите“ трябва да имат профила на същия цикъл, като по този начин предполага, че evo-lyu-that cycle-lo-i-dy е цикъл-lo-i-da със същия pa-ra-met-ra -ми.

В допълнение, предложената Guy-gen-som конструкция на cycl-lo-and-distance-but-no-go pos-vo-la-et on -count дължината на циклите. Ако има синя точка, чиято дължина е равна на това, за което говорите от кръга, огънете нишката възможно най-много, тогава краят й ще бъде в точката на „бузите“ и циклично -tra-преминаване ek-to-rii, т.е. в горната част на цикъла и ди-“бузите”. Тъй като това е половината от дължината на ar-ki cycl-o-i-dy, тогава пълната дължина е равна на кръга на осем ra-di-u-sam pro-iz-vo- dyad.

Christ-an Huy-gens направи cycl-lo-and-distant ma-yat-nik и часове с него pro-ho-di-li-is-py-ta-niya в морето Pu-te-she-stvi - да, но не свикнах. Въпреки това, същото като часовника с обичайния ma-yat-nik за тези цели.

Защо, един към един, все още има часове на кожухална низост между нас и обикновено венозния ма-ят-никой? Ако погледнете, тогава с малки дефекти, като червения, "бузите" циклични и-далеч-но-отидете ma-yat-n-почти нямат влияние. Съответно движението по цикличен и кръгов начин с малки отклонения е почти идентично да, да.

ЛЕМНИКАТИ
Уравнение в полярни координати:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

Ъгъл между AB" или A"B и оста x = 45 o

Площ на един цикъл = a 2 /2

ЦИКЛОИД

Площ на една дъга = 3πa 2

Дължина на дъгата на една арка = 8a

Това е крива, описана от точка P върху окръжност с радиус a, която се търкаля по оста x.

ХИПОЦИКЛОИДИ С ЧЕТИРИ СПИЦИ
Уравнение в правоъгълни координати:
x 2/3 + y 2/3 = a 2/3

Уравнения в параметрична форма:

Площ, оградена от крива = 3πa 2 /8

Дължина на дъгата на цялата крива = 6a

Това е крива, описана от точка P върху окръжност с радиус a/4, която се търкаля вътре в окръжност с радиус a.

КАРДИОИД
Уравнение: r = a(1 + cosθ)

Площ, оградена от крива = 3πa 2 /2

Дължина на дъгата на кривата = 8a

Това е крива, описана от точка P върху окръжност с радиус a, която се търкаля извън окръжността с радиус a. Тази крива също е частен случай на охлюва на Паскал.

ВЕРИЖНА ЛИНИЯ
Уравнението:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Това е кривата, по която една верига ще виси, когато е окачена вертикално от точка А до точка Б.

РОЗА С ТРИ ЛИСТЕНЧЕТА
Уравнение: r = acos3θ

Уравнението r = acos3θ е подобно на кривата, получена чрез въртене обратно на часовниковата стрелка по крива от 30 o или π/6 радиана.

Като цяло, r = acosnθ или r = asinnθ има n дяла, ако n е нечетно.

ЧЕТИРИ ЛИСТЕНЧЕТА РОЗА
Уравнение: r = acos2θ

Уравнението r = asin2θ е подобно на кривата, получена чрез въртене обратно на часовниковата стрелка по крива 45 o или π/4 радиан.

Като цяло r = acosnθ или r = asinnθ има 2n венчелистчета, ако n е четно.

ЕПИЦИКЛОИД
Параметрични уравнения:

Това е кривата, описана от точка P върху окръжност с радиус b, докато се търкаля по външната страна на окръжността с радиус a. Кардиоидата е специален случай на епициклоида.

ОБЩ ХИПОЦИКЛОИД
Параметрични уравнения:

Това е кривата, описана от точка P върху окръжност с радиус b, докато се търкаля по външната страна на окръжността с радиус a.

Ако b = a/4, кривата е хипоциклоида с четири точки.

ТРОХОИД
Параметрични уравнения:

Това е кривата, описана от точка P на разстояние b от центъра на окръжност с радиус a, докато се върти по оста x.
Ако b е съкратена циклоида.
Ако b > a, кривата има формата, показана на фиг. 11-11 и се нарича проходилка.
Ако b = a, кривата е циклоида.

ТРАКТРИЦЕ
Параметрични уравнения:

Това е кривата, описана от крайната точка P на опъната струна с дължина PQ, когато другият край Q се премества по оста x.

VERZIERA (VERZIERA) AGNEZI (ПОНЯКОГА CURL AGNEZI)
Уравнение в правоъгълни координати: y = 8a 3 /(x 2 + 4a 2)

Параметрични уравнения:

B. На фигурата променливата права OA пресича y = 2a и окръжност с радиус a с център (0,a) съответно в A и B. Всяка точка P на "къдрицата" се определя чрез конструиране на линии, успоредни на осите x и y и съответно през B и A, и определяне на пресечната точка на P.

ЛИСТ НА ДЕКАРТ
Уравнение в правоъгълни координати:
x 3 + y 3 = 3axy

Параметрични уравнения:

Зона на контура 3a 2 /2

Асимптотично уравнение: x + y + a = 0.

КРЪГ УЧАСТВАЩ
Параметрични уравнения:

Това е кривата, описана от крайната точка P на нишката, докато се развива от окръжност с радиус a.

ЕЛИПСА ИНВОЛВЕНТА
Уравнение в правоъгълни координати:
(ax) 2/3 + (по) 2/3 = (a 2 - b 2) 2/3

Параметрични уравнения:

Тази крива е обвивката, нормална към елипсата x 2 /a 2 + y 2 /b 2 = 1.

КАСИНИ ОВАЛИ
Полярно уравнение: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.

Това е крива, описана от точка P, така че произведението на нейното разстояние от две фиксирани точки [разстояние 2a отстрани] е константа b 2 .

Крива като на фигурите по-долу, когато b a съответно.

Ако b = a, кривата е лемниската

ОХЛЮВЪТ НА ПАСКАЛ
Полярно уравнение: r = b + acosθ

Нека OQ е правата, свързваща центъра на O с всяка точка Q от окръжност с диаметър a, минаваща през O. Тогава кривата е фокусът на всички точки P, така че PQ = b.

Кривата, показана на фигурите по-долу, когато b > a или b

ЦИСОИД НА ДИОКЛЕС
Уравнение в правоъгълни координати: y 2 = x 3 /(2a - x)

Параметрични уравнения:

Това е крива, описана от точка P, така че разстоянието OP = разстоянието RS. Използва се в задачата удвояване на куба, т.е. намиране на страната на куб, която има два пъти по-голям обем от даден куб

АРХИМЕДОВА СПИРАЛА
Полярно уравнение: r = aθ

Кривата или линията е геометрична концепция, която се дефинира по различен начин в различните раздели.

КРИВА (линия), следа, оставена от движеща се точка или тяло. Обикновено кривата се представя само като плавно извита линия, като парабола или кръг. Но математическото понятие за крива обхваща както права линия, така и фигури, съставени от прави сегменти, например триъгълник или квадрат.

Кривите могат да бъдат разделени на равнинни и пространствени. Равнинна крива, като парабола или права линия, се образува от пресичането на две равнини или равнина и тяло и следователно лежи изцяло в една равнина. Пространствена крива, например спирала, оформена като спирална пружина, не може да се получи като пресечна точка на някаква повърхност или тяло с равнина и не лежи в същата равнина. Кривите също могат да бъдат разделени на затворени и отворени. Затворена крива, като квадрат или кръг, няма краища, т.е. подвижната точка, която генерира такава крива, периодично повтаря своя път.

Кривата е геометрично място или набор от точки, които отговарят на някакво математическо условие или уравнение.

Например окръжността е геометричното място на точки в равнина, които са на еднакво разстояние от дадена точка. Кривите, определени от алгебрични уравнения, се наричат ​​алгебрични криви.

Например, уравнението на права линия y = mx + b, където m е наклонът и b е сегментът, пресечен на оста y, е алгебрично.

Криви, чиито уравнения съдържат трансцендентални функции, като логаритми или тригонометрични функции, се наричат ​​трансцендентални криви.

Например y = log x и y = tan x са уравнения на трансцендентални криви.

Формата на алгебричната крива може да се определи от степента на нейното уравнение, която съвпада с най-високата степен на членовете на уравнението.

Ако уравнението е от първа степен, например Ax + By + C = 0, тогава кривата има формата на права линия.

Ако уравнението от втора степен е, например,

Ax 2 + By + C = 0 или Ax 2 + By 2 + C = 0, тогава кривата е квадратна, т.е. представлява едно от коничните сечения; Тези криви включват параболи, хиперболи, елипси и кръгове.

Нека изброим общите форми на уравненията на коничните сечения:

x 2 + y 2 = r 2 - кръг,

x 2 /a 2 + y 2 /b 2 = 1 - елипса,

y = ax 2 - парабола,

x 2 /a 2 – y 2 /b 2 = 1 - хипербола.

Криви, съответстващи на уравненията на трето, четвърто, пето, шесто и т.н. степени, се наричат ​​криви на трета, четвърта, пета, шеста и т.н. поръчка. Като цяло, колкото по-висока е степента на уравнението, толкова повече завои ще има отворената крива.

Много сложни криви са получили специални имена.

Циклоида е равнинна крива, описана от фиксирана точка върху окръжност, въртяща се по права линия, наречена генератор на циклоидата; циклоидът се състои от поредица от повтарящи се дъги.

Епициклоида е равнинна крива, описана от фиксирана точка върху окръжност, търкаляща се върху друга фиксирана окръжност извън нея.

Хипоциклоида е равнинна крива, описана от фиксирана точка върху окръжност, търкаляща се отвътре по фиксирана окръжност.

Спиралата е плоска крива, която се развива завой по завой от фиксирана точка (или се увива около нея).

Математиците изучават свойствата на кривите от древни времена и имената на много необичайни криви са свързани с имената на тези, които първи са ги изучавали. Това са например спиралата на Архимед, къдренето на Агнези, цисоидът на Диоклес, кохоидът на Никомед и лемниската на Бернули.

В рамките на елементарната геометрия понятието крива не получава ясна формулировка и понякога се определя като „дължина без ширина“ или като „граница на фигура“. По същество в елементарната геометрия изучаването на кривите се свежда до разглеждане на примери (, , , и т.н.). Липсвайки общи методи, елементарната геометрия навлезе доста дълбоко в изследването на свойствата на специфични криви (, някоии също), използвайки специални техники за всеки отделен случай.

Най-често кривата се дефинира като непрекъснато картографиране от сегмент към:

В същото време кривите може да са различни, дори и да сасъвпада. Такива криви се наричатпараметризирани кривиили ако[ а , b ] = , начини.

Понякога кривата се определя до , т.е. до минималната връзка на еквивалентност, така че параметричните криви

са еквивалентни, ако има непрекъснат (понякога ненамаляващ) чот сегмента [ а 1 ,b 1 ] на сегмент [ а 2 ,b 2], така че

Тези, дефинирани от тази връзка, се наричат ​​просто криви.

Аналитични определения

В курсовете по аналитична геометрия е доказано, че сред линии, записани в декартови правоъгълни (или дори общи афинни) координати чрез общо уравнение от втора степен

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(където поне един от коефициентите A, B, C е различен от нула) са намерени само следните осем вида линии:

а) елипса;

б) хипербола;

в) парабола (неизродени криви от втори ред);

г) двойка пресичащи се прави;

д) двойка успоредни прави;

е) двойка съвпадащи прави (една права);

ж) една точка (изродени прави от втори ред);

з) „линия“, която изобщо не съдържа точки.

Обратно, всяка линия от всеки от осемте посочени типа се записва в декартови правоъгълни координати чрез някакво уравнение от втори ред. (В курсовете по аналитична геометрия те обикновено говорят за девет (не осем) вида конични сечения, защото правят разлика между „въображаема елипса“ и „двойка въображаеми успоредни прави“ – геометрично тези „линии“ са еднакви, тъй като и двете правят не съдържат нито една точка, но аналитично се записват с различни уравнения.) Следователно (изродените и неизродените) конични сечения могат също да бъдат определени като линии от втори ред.

INкрива в равнина се дефинира като набор от точки, чиито координати удовлетворяват уравнениетоЕ ( х , г ) = 0 . В същото време за функциятаЕ се налагат ограничения, които гарантират, че това уравнение има безкраен брой различни решения и

този набор от решения не запълва „парчето от самолета“.

Алгебрични криви

Важен клас криви са тези, за които функциятаЕ ( х , г ) Имаот две променливи. В този случай кривата, определена от уравнениетоЕ ( х , г ) = 0 , Наречен.

Алгебричните криви, определени от уравнение от 1-ва степен, са .

Уравнение от степен 2, имащо безкраен брой решения, определя , тоест изродено и неизродено.

Примери за криви, дефинирани от уравнения от 3-та степен: , .

Примери за криви от 4-та степен: и.

Пример за крива от 6-та степен: .

Пример за крива, дефинирана от уравнение с четна степен: (мултифокална).

Разглеждат се алгебрични криви, дефинирани от уравнения от по-високи степени. В същото време тяхната теория става по-хармонична, ако разглеждането се проведе върху. В този случай алгебричната крива се определя от уравнение на формата

Е ( z 1 , z 2 , z 3 ) = 0 ,

Където Е- полином от три променливи, които са точки.

Видове криви

Равнинната крива е крива, в която всички точки лежат в една и съща равнина.

(проста линия или йорданова дъга, също контур) - набор от точки на равнина или пространство, които са в едно към едно и взаимно непрекъснато съответствие с отсечките.

Пътят е сегмент в .

аналитични криви, които не са алгебрични. По-точно, криви, които могат да бъдат дефинирани през линията на нивото на аналитична функция (или, в многомерния случай, система от функции).

синусоида,

циклоид,

Архимедова спирала,

трактор,

верижна линия,

Хиперболична спирала и др.

1. Методи за дефиниране на криви:

аналитичен – кривата е дадена от математическо уравнение;

графичен – кривата се посочва визуално върху графичен носител на информация;

табличен – кривата се определя от координатите на последователна поредица от точки.

параметричен (най-често срещаният начин за определяне на уравнението на крива):

Където - гладки параметрични функцииT, и

(х") 2 + (г") 2 + (z") 2 > 0 (условие за редовност).

Често е удобно да се използва инвариантно и компактно представяне на уравнението на крива, като се използва:

където от лявата страна има точки от кривата, а дясната страна определя нейната зависимост от някакъв параметър T. Разширявайки този запис в координати, получаваме формула (1).

1. Циклоид.

Историята на изследването на циклоида е свързана с имената на такива велики учени, философи, математици и физици като Аристотел, Птолемей, Галилей, Хюйгенс, Торичели и други.

Циклоид(отκυκλοειδής - кръгъл) -, който може да се дефинира като траектория на точка, лежаща на границата на окръжност, търкаляща се без плъзгане по права линия. Този кръг се нарича генериращ.

Един от най-старите методи за формиране на криви е кинематичният метод, при който кривата се получава като траектория на точка. Крива, която се получава като траектория на точка, фиксирана върху окръжност, търкаляща се без плъзгане по права линия, по окръжност или друга крива, се нарича циклоидална, което в превод от гръцки означава кръгла, напомняща кръг.

Нека първо разгледаме случая, когато кръгът се търкаля по права линия. Кривата, описана от точка, фиксирана върху окръжност, търкаляща се без плъзгане по права линия, се нарича циклоида.

Нека кръг с радиус R се търкаля по права линия a. C е точка, фиксирана върху окръжност, в началния момент от време, разположена в позиция A (фиг. 1). Нека начертаем на линия a отсечка AB, равна на дължината на окръжността, т.е. AB = 2 π R. Разделете тази отсечка на 8 равни части с точки A1, A2, ..., A8 = B.

Ясно е, че когато окръжността, търкаляща се по права а, направи един оборот, т.е. се завърта на 360, след което ще заеме позиция (8) и точка C ще се премести от позиция A в позиция B.

Ако кръгът направи половин пълен оборот, т.е. се завърти на 180, тогава ще заеме позиция (4), а точка C ще се премести на най-високата позиция C4.

Ако кръгът се завърти на ъгъл 45, кръгът ще се премести в позиция (1), а точка C ще се премести в позиция C1.

Фигура 1 също показва други точки от циклоидата, съответстващи на останалите ъгли на въртене на кръга, кратни на 45.

Свързвайки построените точки с гладка крива, получаваме участък от циклоидата, съответстващ на един пълен оборот на окръжността. При следващите обороти ще се получат същите сечения, т.е. Циклоидата ще се състои от периодично повтарящ се участък, наречен арка на циклоида.

Нека обърнем внимание на положението на допирателната към циклоидата (фиг. 2). Ако велосипедист се движи по мокър път, тогава капките, падащи от колелото, ще летят тангенциално към циклоида и при липса на щитове могат да опръскат гърба на велосипедиста.

Първият човек, който изучава циклоидата, е Галилео Галилей (1564 – 1642). Той измисли и името му.

Свойства на циклоида:

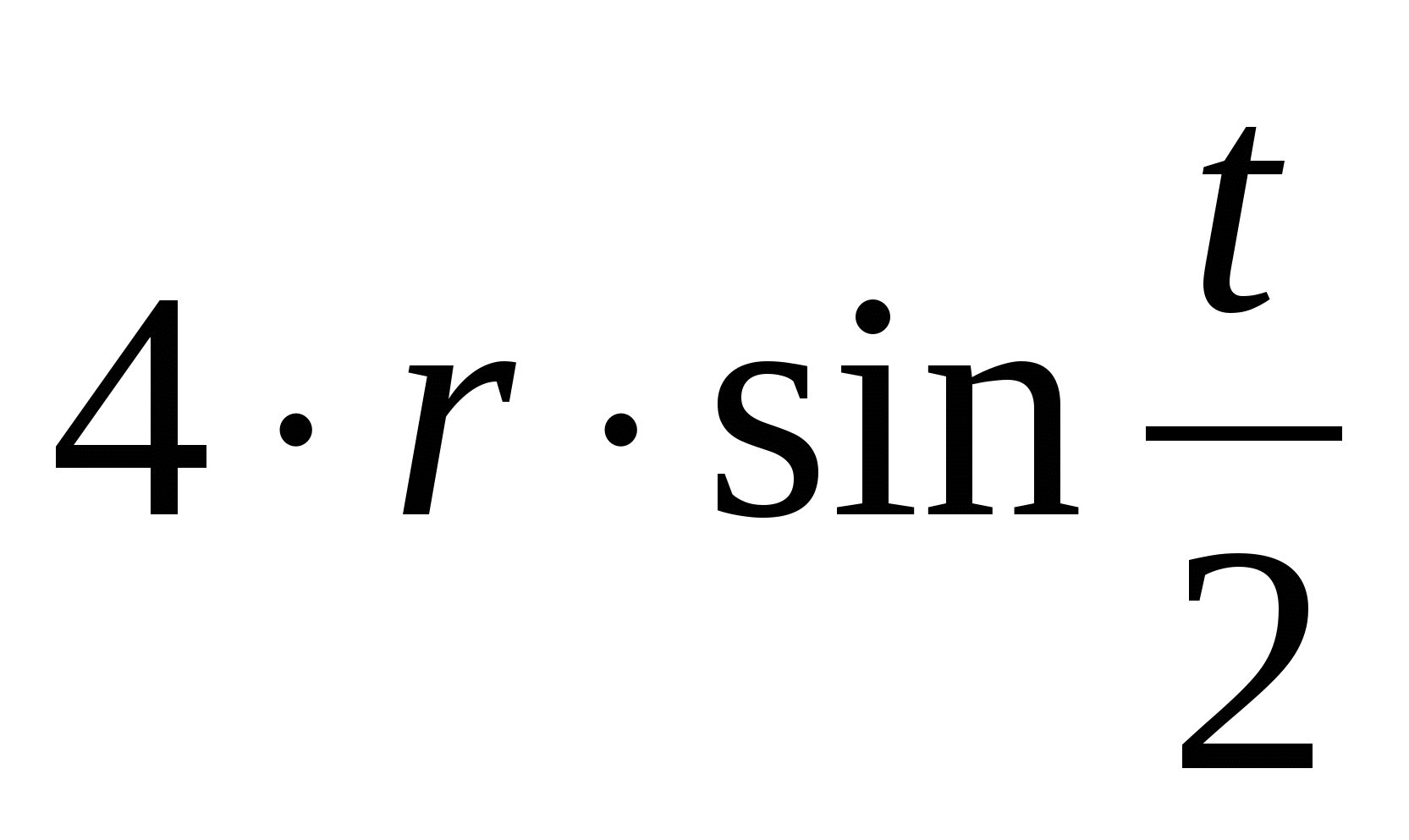
Циклоидът има редица забележителни свойства. Нека споменем някои от тях.

Имот 1. (Ледена планина.) През 1696 г. И. Бернули поставя проблема за намиране на кривата на най-стръмното спускане или, с други думи, проблема за това каква трябва да бъде формата на ледена пързалка, за да се търкаля по нея, за да направи пътуването от началната точка А до крайната точка В за най-кратко време (фиг. 3, а). Желаната крива се нарича "брахистохрон", т.е. крива на най-краткото време.

Ясно е, че най-краткият път от точка А до точка Б е отсечката АВ. Но при такова праволинейно движение скоростта се набира бавно и времето, прекарано при спускане, се оказва голямо (фиг. 3, b).

Колкото по-стръмно е спускането, толкова по-бързо се увеличава скоростта. Но при стръмно спускане пътят по кривата се удължава и по този начин се увеличава времето, необходимо за преминаването му.

Сред математиците, които решават този проблем, са: Г. Лайбниц, И. Нютон, Г. Л'Хопитал и Й. Бернули. Те доказаха, че търсената крива е обърната циклоида (фиг. 3, а). Методите, разработени от тези учени за решаване на проблема с брахистохрона, поставиха основите на ново направление в математиката - вариационното смятане.

Имот 2. (Часовник с махало.) Часовник с обикновено махало не може да работи точно, тъй като периодът на трептене на махалото зависи от неговата амплитуда: колкото по-голяма е амплитудата, толкова по-голям е периодът. Холандският учен Кристиан Хюйгенс (1629 – 1695) се чуди каква крива трябва да следва топката върху връвта на махалото, така че периодът на нейните трептения да не зависи от амплитудата. Обърнете внимание, че при обикновено махало кривата, по която се движи топката, е кръг (фиг. 4).

Кривата, която търсихме, се оказа обърната циклоида. Ако например се направи траншея във формата на обърната циклоида и по нея се пусне топка, тогава периодът на движение на топката под въздействието на гравитацията няма да зависи от първоначалното й положение и амплитуда (фиг. 5 ). За това свойство циклоидът се нарича още „тавтохрон“ - крива на равни времена.

Хюйгенс прави две дървени дъски с ръбове във формата на циклоид, ограничаващи движението на нишката отляво и отдясно (фиг. 6). В този случай самата топка ще се движи по обърната циклоида и по този начин периодът на нейните трептения няма да зависи от амплитудата.

От това свойство на циклоидата в частност следва, че независимо от кое място на ледената пързалка във формата на обърната циклоида започнем спускането си, ще прекараме същото време до крайната точка.

Циклоидно уравнение

1. Удобно е уравнението на циклоидата да се напише чрез α - ъгълът на завъртане на окръжността, изразен в радиани; имайте предвид, че α също е равно на пътя, изминат от образуващата окръжност по права линия.

x=rα– rгрях α

y=r – r cos α

2. Нека вземем хоризонталната координатна ос като права линия, по която се търкаля генериращата окръжност на радиуса r.

Циклоидата се описва с параметрични уравнения

х = rt – rгрях T,

г = r – r cos T.

Уравнение в:

Циклоидата може да се получи чрез решаване на диференциалното уравнение:

Из историята на циклоида

Първият учен, обърнал внимание на циклоидаV, но сериозните изследвания на тази крива започват едва през.

Първият човек, който изучава циклоидата, е Галилео Галилей (1564-1642), известният италиански астроном, физик и педагог. Той също така излезе с името „циклоида“, което означава „напомнящ на кръг“. Самият Галилей не е написал нищо за циклоида, но работата му в тази посока се споменава от учениците и последователите на Галилей: Вивиани, Торичели и др. Торичели, известен физик и изобретател на барометъра, посвети много време на математиката. През Ренесанса няма тесни учени-специалисти. Талантлив човек изучава философия, физика и математика и навсякъде получава интересни резултати и прави големи открития. Малко по-късно от италианците французите възприемат циклоида, наричайки го „рулетка“ или „трохоид“. През 1634 г. Робервал - изобретателят на известната система от везни - изчислява площта, ограничена от арката на циклоида и нейната основа. Съществено изследване на циклоида е извършено от съвременник на Галилей. Сред , т.е. криви, чието уравнение не може да бъде написано под формата на х , г, циклоидът е първият от изследваните.

Написа за циклоида:

Рулетката е толкова често срещана линия, че след правата линия и кръга няма по-често срещана линия; толкова често се очертава пред очите на всички, че човек трябва да се изненада, че древните не са го взели предвид... защото това не е нищо повече от път, описан във въздуха от гвоздея на колело.

Новата крива бързо набира популярност и е подложена на задълбочен анализ, който включва, , Нютон,, братя Бернули и други светила на науката от 17-18 век. На циклоида методите, които се появиха през онези години, бяха активно усъвършенствани. Фактът, че аналитичното изследване на циклоидата се оказа толкова успешно, колкото и анализът на алгебричните криви, направи голямо впечатление и се превърна в важен аргумент в полза на „равноправието“ на алгебричните и трансценденталните криви. Епициклоида

Някои видове циклоиди

Епициклоида - траекторията на точка А, лежаща върху окръжност с диаметър D, която се търкаля без плъзгане по направляваща окръжност с радиус R (външен контакт).

Изграждането на епициклоида се извършва в следната последователност:

От център 0 начертайте спомагателна дъга с радиус равен на 000=R+r;

От точки 01, 02, ...012, както от центрове, начертайте окръжности с радиус r до пресичането им със спомагателни дъги в точки A1, A2, ... A12, които принадлежат на епициклоида.

Хипоциклоида

Хипоциклоида е траекторията на точка А, разположена върху окръжност с диаметър D, която се търкаля без плъзгане по направляваща окръжност с радиус R (вътрешно допиране).

Изграждането на хипоциклоида се извършва в следната последователност:

Пораждащата окръжност с радиус r и насочващата окръжност с радиус R са начертани така, че да се допират в точка А;

Пораждащата окръжност се разделя на 12 равни части, получават се точки 1, 2, ... 12;

От център 0 начертайте спомагателна дъга с радиус равен на 000=R-r;

Централният ъгъл a се определя по формулата a =360r/R.

Разделете дъгата на водещата окръжност, ограничена от ъгъл a, на 12 равни части, като получите точки 11, 21, ...121;

От център 0 се изчертават прави линии през точки 11, 21, ...121 до пресичането им със спомагателната дъга в точки 01, 02, ...012;

От център 0 се изчертават спомагателни дъги през разделителни точки 1, 2, ... 12 на генериращата окръжност;

От точки 01, 02, ...012, както от центрове, начертайте окръжности с радиус r до пресичането им със спомагателни дъги в точки A1, A2, ... A12, които принадлежат на хипоциклоидата.

1. Кардиоид.

Кардиоид ( καρδία - сърце, Терминът "кардиоид" е въведен от Кастилон през 1741 г.

Ако вземем окръжност и точка върху нея за полюс, тогава ще получим кардиоида само ако начертаем сегменти, равни на диаметъра на окръжността. За други размери на отложените сегменти, конхоидите ще бъдат удължени или скъсени кардиоиди. Тези удължени и скъсени кардиоиди иначе се наричат ​​кохлея на Паскал.

Кардиоидът има различни приложения в технологиите. Кардиоидните форми се използват за направата на ексцентрици и гърбици за автомобили. Понякога се използва при чертане на зъбни колела. Освен това се използва в оптичната техника.

Свойства на кардиоида

кардиоиден -B M върху движеща се окръжност ще опише затворена траектория. Тази плоска крива се нарича кардиоида.

2) Кардиоидът може да се получи и по друг начин. Маркирайте точка върху кръга ОТНОСНОи нека начертаем лъч от него. Ако от точка Апресичане на този лъч с окръжност, начертайте сегмент сутринта,дължина, равна на диаметъра на окръжността, и лъчът се върти около точката ОТНОСНО, след това точка Мще се движи по кардиоидата.

3) Кардиоидата може също да бъде представена като крива, допирателна към всички окръжности, които имат центрове в дадена окръжност и минават през нейната фиксирана точка. Когато са построени няколко кръга, кардиоидът изглежда като че ли е конструиран сам по себе си.

4) Има също толкова елегантен и неочакван начин да видите кардиоида. На фигурата можете да видите точков източник на светлина върху кръг. След като светлинните лъчи се отразят за първи път от окръжността, те преминават по допирателна към кардиоида. Представете си сега, че кръгът е ръбовете на чашата; ярка крушка се отразява в една точка. Черно кафе се излива в чашата, което ви позволява да видите ярките отразени лъчи. В резултат на това кардиоидът се подчертава от лъчи светлина.

1. Астроид.

Астроид (от гръцки astron - звезда и eidos - изглед), плоска крива, описана от точка на окръжност, която докосва отвътре фиксирана окръжност с четири пъти радиуса и се търкаля по нея, без да се плъзга. Принадлежи към хипоциклоидите. Astroid е алгебрична крива от 6-ти ред.

Астроид.

Дължината на целия астроид е равна на шест радиуса на неподвижния кръг, а ограничената от него площ е три осми от неподвижния кръг.

Допирателната отсечка към астроида, затворена между два взаимно перпендикулярни радиуса на неподвижната окръжност, начертана в върховете на астроида, е равна на радиуса на неподвижната окръжност, независимо от това как е избрана точката.

Свойства на астроида

Има четирикаспа .

Дължина на дъгата от точка 0 до обвивката

семейства от сегменти с постоянна дължина, краищата на които са разположени на две взаимно перпендикулярни линии.

Astroid е от 6-ти ред.

Астроидни уравнения

Уравнение в декартови правоъгълни координати:| x | 2/3 + | y | 2/3 = R 2/3параметрично уравнение:x = Rcos 3 t y = Rsin 3 t

Метод за конструиране на астроид

Начертаваме две взаимно перпендикулярни прави линии и начертаваме поредица от сегменти с дължинаР , чиито краища лежат на тези прави. Фигурата показва 12 такива сегмента (включително сегменти от самите взаимно перпендикулярни прави линии). Колкото повече сегменти начертаем, толкова по-точна ще получим кривата. Нека сега конструираме обвивката на всички тези сегменти. Този плик ще бъде астроидът.

1. Заключение

Работата предоставя примери за задачи с различни видове криви, дефинирани от различни уравнения или отговарящи на някакво математическо условие. По-специално, циклоидални криви, методи за определянето им, различни методи за конструиране, свойства на тези криви.

Свойствата на циклоидалните криви се използват много често в механиката на зъбните колела, което значително увеличава якостта на частите в механизмите.

Цикломида (от гръцки хклпеидЮт - кръгъл) е плоска трансцендентална крива. Циклоида се дефинира кинематично като траектория на фиксирана точка на генерираща окръжност с радиус r, търкаляща се без плъзгане по права линия.

Уравнения

Нека вземем хоризонталната координатна ос като права линия, по която се търкаля образуващата окръжност с радиус r.

· Циклоидата се описва с параметрични уравнения

Уравнение в декартови координати:

· Циклоидата може да се получи като решение на диференциалното уравнение:

Имоти

• · циклоид --периодична функция по оста x, с период 2рr. За граници на периода е удобно да се вземат особени точки (точки на връщане) от вида t = 2рk, където k е произволно цяло число.
• · За да начертаете допирателна към циклоида в произволна точка A, достатъчно е да свържете тази точка с горната точка на образуващата окръжност. Като свържем A с долната точка на генериращата окръжност, получаваме нормалата.
• · Дължината на циклоидната дъга е 8r. Това свойство е открито от Кристофър Рен (1658 г.).
• · Площта под всяка дъга на циклоида е три пъти по-голяма от площта на генериращата окръжност. Торичели твърди, че този факт е открит от Галилей.
• · Радиусът на кривината на първата дъга на циклоидата е равен.

• · “Обърнатата” циклоида е крива с най-стръмно спускане (брахистохрона). Освен това, той също има свойството на таухрония: тежко тяло, поставено във всяка точка на циклоидната дъга, достига хоризонтала за същото време.
• · Периодът на трептене на материална точка, плъзгаща се по обърната циклоида, не зависи от амплитудата; този факт е използван от Хюйгенс за създаване на прецизни механични часовници.
• · Еволютата на циклоида е циклоида, конгруентна на оригиналната, а именно паралелно изместена, така че върховете да се превърнат в „точки“.
• · Машинни части, които едновременно извършват равномерно въртеливо и транслационно движение, описват циклоидални криви (циклоида, епициклоида, хипоциклоида, трохоида, астроида) (срв. конструкцията на лемниската на Бернули).