(μετάφραση από τα ελληνικά. εγκύκλιος) – μια επίπεδη υπερβατική καμπύλη, η οποία περιγράφεται από ένα σημείο σε έναν κύκλο ακτίνας rκύλιση κατά μήκος μιας ευθείας γραμμής χωρίς ολίσθηση (μια υπερβατική καμπύλη είναι μια καμπύλη που δεν μπορεί να περιγραφεί με μια αλγεβρική εξίσωση σε ορθογώνιες συντεταγμένες). Η παραμετρική του εξίσωση

Χ = rt – r αμαρτία t,
y= r - r cos t

Τα σημεία τομής του κυκλοειδούς με την ευθεία γραμμή κατά μήκος της οποίας κυλάει ο κύκλος (αυτός ο κύκλος ονομάζεται κύκλος δημιουργίας και η ευθεία γραμμή κατά μήκος της οποίας κυλά ονομάζεται οδηγός) ονομάζονται σημεία αιχμής και τα υψηλότερα σημεία του κυκλοειδούς , που βρίσκονται στη μέση μεταξύ γειτονικών ακραίων σημείων, ονομάζονται κορυφές του κυκλοειδούς.

Ο Galileo Galilei ήταν ο πρώτος που μελέτησε το κυκλοειδές. Το μήκος ενός κυκλοειδούς τόξου καθορίστηκε το 1658 από τον Άγγλο αρχιτέκτονα και μαθηματικό Christopher Wren, τον συγγραφέα του σχεδιασμού και του κατασκευαστή του τρούλου του καθεδρικού ναού του Αγίου Παύλου στο Λονδίνο. Αποδείχθηκε ότι το μήκος του κυκλοειδούς είναι ίσο με 8 ακτίνες του κύκλου δημιουργίας.
Μία από τις αξιοσημείωτες ιδιότητες του κυκλοειδούς, που του έδωσε το όνομά του - βραχιστοχρόνος (από τις ελληνικές λέξεις "συντομότερο" και "χρόνος") συνδέεται με την επίλυση του προβλήματος της πιο απότομης κατάβασης. Προέκυψε το ερώτημα τι σχήμα πρέπει να δοθεί σε μια καλά γυαλισμένη (για την ουσιαστική εξάλειψη της τριβής) αυλάκωση που συνδέει δύο σημεία έτσι ώστε η μπάλα να κυλήσει από το ένα σημείο στο άλλο στο συντομότερο δυνατό χρόνο. Οι αδερφοί Μπερνούλι απέδειξαν ότι η τάφρος πρέπει να έχει το σχήμα ενός καθοδικού κυκλοειδούς.

Οι καμπύλες που σχετίζονται με το κυκλοειδές μπορούν να ληφθούν λαμβάνοντας υπόψη τις τροχιές των σημείων που δεν βρίσκονται στον κύκλο παραγωγής.

Αφήστε το θέμα Από 0είναι μέσα στον κύκλο. Αν μεταφερθεί Από 0βοηθητικός κύκλος με το ίδιο κέντρο με τον κύκλο παραγωγής, τότε όταν ο κύκλος δημιουργίας κυλά κατά μήκος μιας ευθείας γραμμής ΑΒένας μικρός κύκλος θα κυλήσει σε ευθεία γραμμή ΕΝΑ´ ΣΕ´, αλλά η κύλισή του θα συνοδεύεται από ολίσθηση και τελεία Από 0περιγράφει μια καμπύλη που ονομάζεται συντομευμένο κυκλοειδές.

Ένα επίμηκες κυκλοειδές ορίζεται με παρόμοιο τρόπο - αυτή είναι η τροχιά ενός σημείου που βρίσκεται σε μια επέκταση της ακτίνας του κύκλου παραγωγής, ενώ η κύλιση συνοδεύεται από ολίσθηση προς την αντίθετη κατεύθυνση.

Οι κυκλοειδείς καμπύλες χρησιμοποιούνται σε πολλούς τεχνικούς υπολογισμούς και οι ιδιότητές τους χρησιμοποιούνται, για παράδειγμα, στην κατασκευή προφίλ δοντιών γραναζιών, σε κυκλοειδή εκκρεμή, στην οπτική και, επομένως, η μελέτη αυτών των καμπυλών είναι σημαντική από εφαρμοσμένη άποψη. Εξίσου σημαντικό είναι ότι, μελετώντας αυτές τις καμπύλες και τις ιδιότητές τους, οι επιστήμονες του 17ου αι. ανέπτυξε τεχνικές που οδήγησαν στη δημιουργία διαφορικού και ολοκληρωτικού λογισμού και το πρόβλημα του βραχυστόχρονου ήταν ένα βήμα προς την εφεύρεση του λογισμού των παραλλαγών.

Έλενα Μαλισέφσκαγια

Θυμηθείτε αυτά τα πορτοκαλί πλαστικά ka-ta-fo-you - φως-από-ra-zha-te-li, κολλημένα-la-yu-schi-e-sya στις ακτίνες του ve-lo-si-ped-no- πάω κο-λε-σα; Συνδέστε το ka-ta-fot στο ίδιο το χείλος του ko-le-sa και ακολουθήστε το tra-ek-to-ri-ey του. Οι λαμβανόμενες καμπύλες βρίσκονται στην κορυφή της οικογένειας των κυκλοειδών.

Ταυτόχρονα, το co-le-so ονομάζεται pro-from-a-circle (ή κύκλος) ενός cycl-o-i-dy.

Ας πάμε όμως πίσω στον αιώνα μας και ας στραφούμε σε πιο σύγχρονη τεχνολογία. Στο δρόμο έπεσε ένα κα-μου-σεκ, το οποίο κόλλησε στη ροή του κο-λε-σα. Έχοντας γυρίσει μερικούς κύκλους με τον τροχό, πού πάει η πέτρα όταν πηδάτε έξω από τη ροή; Κόντρα στη δεξιά κίνηση της μοτοσικλέτας ή κατά μήκος της δεξιάς πλευράς;

Όπως γνωρίζετε, η ελεύθερη κίνηση του σώματος είναι καθ' οδόν κατά μήκος της διαδρομής προς εκείνη την τροχιά κατά την οποία στη συνέχεια κινήθηκε. Το ka-sa-tel-naya προς το cycl-o-i-de είναι πάντα προς τα δεξιά κατά μήκος της κατεύθυνσης της κίνησης και διέρχεται από το πάνω σημείο ku σχετικά με τη γύρω περιοχή. Σύμφωνα με τη δεξιά κατεύθυνση κίνησης, το ka-mu-shek μας κινείται επίσης κατά μήκος.

Θυμάστε πώς περπατούσατε μέσα από τις λακκούβες στην παιδική ηλικία με ένα ποδήλατο χωρίς πίσω φτερό; Το υγρό σερί στην πλάτη σου είναι η επιβεβαίωση της προσδοκίας της ζωής ότι μόλις έλαβε ένα ρε-ζουλ -τα-τα.

Ο 17ος αιώνας είναι ο αιώνας του κύκλου. Οι καλύτεροι επιστήμονες έχουν μελετήσει τις εκπληκτικές του ιδιότητες.

Κάποιο είδος tra-ec-to-ria θα φέρει το σώμα, κινούμενο υπό τη δράση της δύναμης της βαρύτητας, από το ένα σημείο στο άλλο σε σύντομο χρονικό διάστημα; Αυτό ήταν ένα από τα πρώτα καθήκοντα εκείνου του na-u-ki, το οποίο έχει τώρα το όνομα va-ri-a-tsi-on-noe.

Mi-ni-mi-zi-ro-vat (ή max-si-mi-zi-ro-vat) μπορείτε να έχετε διαφορετικά πράγματα - μήκος διαδρομής, ταχύτητα, χρόνο. Στο za-da-che σχετικά με το bra-hi-sto-khron mi-ni-mi-zi-ru-et-sya είναι καιρός (ό,τι ο διάολος-κι-βα-ετ-σιά σα-μίμε στο -όνομα: Ελληνικά βράχιστος - ελάχιστος, χρόνος - χρόνος).

Το πρώτο πράγμα που έρχεται στο μυαλό είναι η ευθεία γραμμή tra-ek-to-ria. Ναι, θα εξετάσουμε επίσης τον κύκλο επαναφοράς με το σημείο επιστροφής στην κορυφή των δεδομένων σημείων. Και, ακολουθώντας το Ga-li-leo Ga-li-le-em, - ένας τέταρτος κατακόρυφος κύκλος που συνδέει τα σημεία μας.

Γιατί ο Ga-li-leo Ga-li-lei κοίταξε τον κατακόρυφο κύκλο και σκέφτηκε ότι αυτή ήταν η καλύτερη κατά την έννοια κάθοδος; Έγραψε σπασμένα σε αυτό και παρατήρησε ότι όσο αυξανόταν ο αριθμός των συνδέσμων, ο χρόνος αργότερα μειώθηκε. Από εδώ, ο Ga-li-ley κινήθηκε φυσικά στον κύκλο, αλλά έβγαλε το λάθος συμπέρασμα ότι αυτό το tra-ek -ria είναι το καλύτερο από όλα τα πιθανά. Όπως βλέπουμε, το καλύτερο tra-ek-to-ri-ey είναι ένα cycl-o-i-da.

Μέσω δύο δεδομένων σημείων είναι δυνατό να δημιουργηθεί ένας μόνο κύκλος με την προϋπόθεση ότι στο πάνω σημείο υπάρχει σημείο επιστροφής του κύκλου. Και ακόμα κι όταν ο κύκλος μπει κάτω από τη μαμά για να περάσει από το δεύτερο σημείο, θα εξακολουθεί να ουρλιάζει από την πιο γρήγορη κατάβαση!

Ένα άλλο όμορφο za-da-cha, που συνδέεται με το cycl-lo-i-da, - za-da-cha για το ta-u-to-chron. Μετάφραση από τα ελληνικά, ταύτις σημαίνει «το ίδιο», χρόνος, όπως ήδη γνωρίζουμε, «χρόνος».

Θα φτιάξουμε τρεις λόφους ένας προς έναν με ένα pro-fi-lem σε μορφή κύκλων, έτσι ώστε τα άκρα των λόφων να ευθυγραμμίζονται και να εδράζονται στην κορυφή του κύκλου. Στήσαμε τρία bo-bahs για διαφορετικούς εσένα και ας προχωρήσουμε. Είναι εκπληκτικό το γεγονός ότι όλοι θα κατέβουν μια μέρα!

Το χειμώνα, μπορείτε να φτιάξετε μια τσουλήθρα με πάγο στην αυλή σας και να ελέγξετε αυτό το ακίνητο ζωντανά.

Για-ναι-χα-σχετικά-ότι-χρόνο-είναι-στο-look-up-της-ίδιας-καμπύλης που, ξεκινώντας από οποιαδήποτε-αρχή- Αλλά στο κάτω-κάτω, ο χρόνος καθόδου στο δεδομένο το σημείο θα είναι το ίδιο.

Ο Christian Guy-gens ξέρει ότι το μόνο που είναι χρόνιο είναι το κυκλικό.

Φυσικά, ο Guy-gen-sa δεν κάνει την κάθοδο κατά μήκος των παγωμένων βουνών. Εκείνη την εποχή, οι επιστήμονες δεν είχαν τόσο μεγάλη αγάπη για την τέχνη. Για-ναι-που-έχουμε-μελετηθεί,-είναι-χο-ντι-από τη ζωή και για-υπέρ εκείνων των καιρών. Τον 17ο αιώνα είχαν ήδη ολοκληρωθεί τα θαλάσσια ταξίδια μεγάλων αποστάσεων. Ο Shi-ro-tu sea-rya-ki ήταν ήδη σε θέση να προσδιορίσει έως και εκατό με ακρίβεια, αλλά είναι εκπληκτικό το γεγονός ότι για μεγάλο χρονικό διάστημα δεν μπορούσαν να προσδιορίσουν - να αντιμετωπίσουν τα πάντα. Και μια από τις μεθόδους pre-la-gav-shih από το shi-ro-you βασίστηκε στην παρουσία ακριβούς chro-no-meth τάφρου

Ο πρώτος που σκέφτηκε να φτιάξει ma-yat-no-no-new-ρολόγια που θα ήταν ακριβείς ήταν ο Ga-li-leo Ga-li-ley. Ωστόσο, τη στιγμή που αρχίζει να τα ξαναδημιουργεί, είναι ήδη ηλικιωμένος, είναι τυφλός και στον υπόλοιπο χρόνο ο επιστήμονας δεν έχει χρόνο να ολοκληρώσει τη ζωή του. Το λέει αυτό στον γιο του, αλλά εκείνος διστάζει και αρχίζει να π--------------------------- κοντά στο θάνατο και δεν προλαβαίνει να καθίσει κάτω. Η επόμενη διάσημη φιγούρα ήταν ο Christian Huygens.

Παρατήρησε ότι η περίοδος του ko-le-ba-niya συνήθως ma-yat-ni-ka, ras-smat-ri-vav-she-go-sya Ga-li-le-em, za-vis-sit από- from-the-start-of-the-lo-zhe-niya, δηλ. από am-pl-tu-dy. Σκεπτόμενος ποια πρέπει να είναι η τροχιά της κίνησης του φορτίου ώστε ο χρόνος να μην εξαρτάται από αυτήν -se-lo από am-pl-tu-dy, αποφασίζει για-da-chu σχετικά με το ότι-u-to-chron. Αλλά πώς μπορείτε να κάνετε το φορτίο να κινείται με κυκλικό τρόπο; Μετάφραση των σπουδών theo-re-ti-che-re-studies σε ένα πρακτικά-ti-che-plane, Guy-gens de-la-et “cheeks” , στο οποίο on-ma-you-va-et-sya ve- rev-ka ma-yat-no-ka, και αποφασίζει μερικές ακόμη εργασίες ma-te-ma-ti-che -skih. Υποστηρίζει ότι τα «μάγουλα» πρέπει να έχουν το προφίλ του ίδιου κύκλου, υποδηλώνοντας έτσι ότι το evo-lyu-that cycle-lo-i-dy είναι ένας κύκλος-lo-i-da με το ίδιο pa-ra-met-ra -μι.

Επιπλέον, η προτεινόμενη κατασκευή Guy-gen-som ενός κυκλικού-lo-and-distance-but-no-go pos-vo-la-et on-μετράει τη διάρκεια των κύκλων. Εάν υπάρχει ένα μπλε σημείο, το μήκος του οποίου είναι ίσο με αυτό για το οποίο μιλάτε από τον κύκλο, λυγίστε το νήμα όσο το δυνατόν περισσότερο, τότε το άκρο του θα είναι στο σημείο των «μάγουλων» και θα είναι κυκλικό. -tra-crossing ek-to-rii, δηλ. στην κορυφή του κύκλου-και-δύ-«μάγουλα». Εφόσον αυτό είναι το μισό του μήκους του ar-ki cycl-o-i-dy, τότε το πλήρες μήκος είναι ίσο με οκτώ κύκλους ra-di-u-sam pro-iz-vo-dyad.

Ο Christ-an Huy-gens έφτιαξε ένα κυκλικό και μακρινό ma-yat-nik και ώρες μαζί του pro-ho-di-li-is-py-ta-niya στη θάλασσα Pu-te-she-stvi -ναι, αλλά δεν το συνήθισα. Ωστόσο, το ίδιο με το ρολόι με το συνηθισμένο ma-yat-nik για αυτούς τους σκοπούς.

Γιατί, ένας προς έναν, υπάρχουν ακόμα ώρες γούνας ανάμεσα σε εμάς και τον συνήθως φλεβωμένο ma-yat-no-one; Αν κοιτάξετε, τότε με μικρά ελαττώματα, όπως το κόκκινο, τα «μάγουλα» κυκλικά και-μακριά-αλλά-πάνε ma-yat-n-σχεδόν δεν έχουν καμία επιρροή. Αντίστοιχα, η κίνηση με κυκλικό και κυκλικό τρόπο με μικρές αποκλίσεις είναι σχεδόν πανομοιότυπη ναι, ναι.

ΛΕΜΝΙΚΑΤΕΣ
Εξίσωση σε πολικές συντεταγμένες:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

Γωνία μεταξύ ΑΒ" ή Α"Β και άξονα x = 45 o

Περιοχή ενός βρόχου = a 2/2

ΚΥΚΛΟΕΙΔΗΣ

Εμβαδόν ενός τόξου = 3πa 2

Μήκος τόξου ενός τόξου = 8α

Αυτή είναι μια καμπύλη που περιγράφεται από ένα σημείο P σε έναν κύκλο ακτίνας a, που κυλά κατά μήκος του άξονα x.

ΥΠΟΚΥΚΛΟΕΙΔΗ ΜΕ ΤΕΣΣΕΡΙΣ ΑΚΙΤΕΣ
Εξίσωση σε ορθογώνιες συντεταγμένες:
x 2/3 + y 2/3 = a 2/3

Εξισώσεις σε παραμετρική μορφή:

Εμβαδόν που περικλείεται από καμπύλη = 3πa 2 /8

Μήκος τόξου ολόκληρης της καμπύλης = 6a

Αυτή είναι μια καμπύλη που περιγράφεται από ένα σημείο P σε έναν κύκλο ακτίνας a/4, το οποίο κυλά μέσα σε έναν κύκλο ακτίνας a.

ΚΑΡΔΙΟΕΙΔΗ
Εξίσωση: r = a(1 + cosθ)

Εμβαδόν που περικλείεται από καμπύλη = 3πa 2 /2

Μήκος τόξου καμπύλης = 8a

Είναι μια καμπύλη που περιγράφεται από ένα σημείο P σε έναν κύκλο ακτίνας a, το οποίο κυλά έξω από τον κύκλο της ακτίνας a. Αυτή η καμπύλη είναι επίσης μια ειδική περίπτωση του σαλιγκαριού του Pascal.

ΓΡΑΜΜΗ ΑΛΥΣΙΔΑΣ
Η εξίσωση:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Αυτή είναι η καμπύλη κατά μήκος της οποίας μια αλυσίδα θα κρεμόταν κάθετα από το σημείο Α στο Β.

ΤΡΙΑΝΤΑΦΥΛΛΟ ΜΕ ΤΡΙΑ ΠΕΤΑΛΑ
Εξίσωση: r = acos3θ

Η εξίσωση r = acos3θ είναι παρόμοια με την καμπύλη που προκύπτει περιστρέφοντας αριστερόστροφα κατά μήκος μιας καμπύλης 30 o ή π/6 ακτίνων.

Γενικά, το r = acosnθ ή r = asinnθ έχει n πέταλα αν το n είναι περιττό.

ΤΕΣΣΕΡΑ ΠΕΤΑΛΑ ΤΡΙΑΝΤΑΦΥΛΛΟ
Εξίσωση: r = acos2θ

Η εξίσωση r = asin2θ είναι παρόμοια με την καμπύλη που προκύπτει περιστρέφοντας αριστερόστροφα κατά μήκος μιας καμπύλης 45 o ή π/4 ακτίνων.

Γενικά r = acosnθ ή r = asinnθ έχει 2n πέταλα αν το n είναι άρτιο.

ΕΠΙΚΥΚΛΟΕΙΔΗ
Παραμετρικές εξισώσεις:

Είναι η καμπύλη που περιγράφεται από το σημείο P σε έναν κύκλο ακτίνας b καθώς κυλίεται κατά μήκος του εξωτερικού του κύκλου ακτίνας a. Το καρδιοειδές είναι μια ειδική περίπτωση επικυκλοειδούς.

ΓΕΝΙΚΟ ΥΠΟΚΥΚΛΟΕΙΔΗ
Παραμετρικές εξισώσεις:

Είναι η καμπύλη που περιγράφεται από το σημείο P σε έναν κύκλο ακτίνας b καθώς κυλίεται κατά μήκος του εξωτερικού του κύκλου ακτίνας a.

Αν b = a/4, η καμπύλη είναι ένα υποκυκλοειδές με τέσσερα σημεία.

ΤΡΟΧΟΕΙΔΗ
Παραμετρικές εξισώσεις:

Αυτή είναι η καμπύλη που περιγράφεται από το σημείο P σε απόσταση b από το κέντρο ενός κύκλου ακτίνας a καθώς κυλίεται κατά μήκος του άξονα x.
Αν το b είναι βραχυμένο κυκλοειδές.
Εάν b > a, η καμπύλη έχει το σχήμα που φαίνεται στο Σχ. 11-11 και καλείται περιπατητής.
Αν b = a, η καμπύλη είναι κυκλοειδής.

TRAKTRICE
Παραμετρικές εξισώσεις:

Είναι η καμπύλη που περιγράφεται από το τελικό σημείο P μιας τεντωμένης χορδής μήκους PQ όταν το άλλο άκρο Q μετακινείται κατά μήκος του άξονα x.

ΒΕΡΖΙΕΡΑ (ΒΕΡΖΙΕΡΑ) ΑΓΝΕΖΗ (ΚΑΜΙΑ ΦΟΡΕΣ ΚΟΥΡΛ ΑΓΝΕΖΗ)
Εξίσωση σε ορθογώνιες συντεταγμένες: y = 8a 3 /(x 2 + 4a 2)

Παραμετρικές εξισώσεις:

Β. Στο σχήμα, η μεταβλητή ευθεία ΟΑ τέμνει το y = 2a και έναν κύκλο με ακτίνα a με κέντρο (0,a) στο Α και Β, αντίστοιχα. Οποιοδήποτε σημείο P στην "καμπούλα" προσδιορίζεται κατασκευάζοντας ευθείες παράλληλες στους άξονες x και y, και μέσω των B και A αντίστοιχα, και ορίζοντας το σημείο τομής του P.

ΦΥΛΛΟ DESCARTES
Εξίσωση σε ορθογώνιες συντεταγμένες:
x 3 + y 3 = 3αξον

Παραμετρικές εξισώσεις:

Περιοχή βρόχου 3a 2 /2

Ασύμπτωτη εξίσωση: x + y + a = 0.

ΚΥΚΛΟΣ ΕΜΠΛΕΚΤΟΣ
Παραμετρικές εξισώσεις:

Αυτή είναι η καμπύλη που περιγράφεται από το τελικό σημείο P της χορδής καθώς ξετυλίγεται από έναν κύκλο ακτίνας a.

ΕΛΛΕΙΨΗ ΕΜΠΛΕΚΤ
Εξίσωση σε ορθογώνιες συντεταγμένες:
(ax) 2/3 + (by) 2/3 = (a 2 - b 2) 2/3

Παραμετρικές εξισώσεις:

Αυτή η καμπύλη είναι το περίβλημα κάθετο προς την έλλειψη x 2 /a 2 + y 2 /b 2 = 1.

ΚΑΣΙΝΙ ΟΒΑΛ
Πολική εξίσωση: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.

Είναι μια καμπύλη που περιγράφεται από ένα σημείο P έτσι ώστε το γινόμενο της απόστασής της από δύο σταθερά σημεία [απόσταση 2a από την πλευρά] να είναι μια σταθερά b 2 .

Καμπύλη όπως στα παρακάτω σχήματα όταν b a αντίστοιχα.

Αν b = a, η καμπύλη είναι λεμνίσκατ

ΤΟ ΣΑΛΙΓΚΙ ΤΟΥ ΠΑΣΚΑΛ
Πολική εξίσωση: r = b + acosθ

Έστω OQ η ευθεία που συνδέει το κέντρο του O με οποιοδήποτε σημείο Q σε κύκλο διαμέτρου a που διέρχεται από το O. Τότε η καμπύλη είναι η εστίαση όλων των σημείων P έτσι ώστε PQ = b.

Η καμπύλη που φαίνεται στα παρακάτω σχήματα όταν b > a ή b

ΚΙΣΣΟΕΙΔΗ ΔΙΟΚΛΩΝ
Εξίσωση σε ορθογώνιες συντεταγμένες: y 2 = x 3 /(2a - x)

Παραμετρικές εξισώσεις:

Αυτή είναι μια καμπύλη που περιγράφεται από ένα σημείο P έτσι ώστε απόσταση OP = απόσταση RS. Χρησιμοποιείται στην εργασία διπλασιάζοντας τον κύβο, δηλ. βρίσκοντας την πλευρά ενός κύβου που έχει διπλάσιο όγκο από έναν δεδομένο κύβο

ΣΠΕΙΡΑ ΑΡΧΙΜΗΔΗ
Πολική εξίσωση: r = aθ

Η καμπύλη ή η γραμμή είναι μια γεωμετρική έννοια που ορίζεται διαφορετικά σε διαφορετικά τμήματα.

ΚΑΜΠΥΛΗ (γραμμή), ίχνος που αφήνει ένα κινούμενο σημείο ή σώμα. Συνήθως μια καμπύλη αναπαρίσταται μόνο ως μια ομαλά καμπυλωτή γραμμή, όπως μια παραβολή ή ένας κύκλος. Αλλά η μαθηματική έννοια της καμπύλης καλύπτει τόσο μια ευθεία γραμμή όσο και τα σχήματα που αποτελούνται από ευθύγραμμα τμήματα, για παράδειγμα, ένα τρίγωνο ή ένα τετράγωνο.

Οι καμπύλες μπορούν να χωριστούν σε επίπεδες και χωρικές. Μια επίπεδη καμπύλη, όπως μια παραβολή ή μια ευθεία γραμμή, σχηματίζεται από την τομή δύο επιπέδων ή ενός επιπέδου και ενός σώματος και επομένως βρίσκεται εξ ολοκλήρου σε ένα επίπεδο. Μια χωρική καμπύλη, για παράδειγμα, μια έλικα σε σχήμα ελικοειδούς ελατηρίου, δεν μπορεί να ληφθεί ως τομή κάποιας επιφάνειας ή σώματος με ένα επίπεδο και δεν βρίσκεται στο ίδιο επίπεδο. Οι καμπύλες μπορούν επίσης να χωριστούν σε κλειστές και ανοιχτές. Μια κλειστή καμπύλη, όπως ένα τετράγωνο ή ένας κύκλος, δεν έχει άκρα, δηλ. το κινούμενο σημείο που δημιουργεί μια τέτοια καμπύλη επαναλαμβάνει περιοδικά τη διαδρομή του.

Μια καμπύλη είναι ένας τόπος, ή σύνολο, σημείων που ικανοποιούν κάποια μαθηματική συνθήκη ή εξίσωση.

Για παράδειγμα, ένας κύκλος είναι ο τόπος των σημείων σε ένα επίπεδο που απέχουν ίση από ένα δεδομένο σημείο. Οι καμπύλες που ορίζονται από αλγεβρικές εξισώσεις ονομάζονται αλγεβρικές καμπύλες.

Για παράδειγμα, η εξίσωση μιας ευθείας y = mx + b, όπου m είναι η κλίση και b είναι το τμήμα που τέμνεται στον άξονα y, είναι αλγεβρική.

Οι καμπύλες των οποίων οι εξισώσεις περιέχουν υπερβατικές συναρτήσεις, όπως λογάριθμους ή τριγωνομετρικές συναρτήσεις, ονομάζονται υπερβατικές καμπύλες.

Για παράδειγμα, y = log x και y = tan x είναι εξισώσεις υπερβατικών καμπυλών.

Το σχήμα μιας αλγεβρικής καμπύλης μπορεί να προσδιοριστεί από το βαθμό της εξίσωσής της, που συμπίπτει με τον υψηλότερο βαθμό των όρων της εξίσωσης.

Αν η εξίσωση είναι πρώτου βαθμού, για παράδειγμα Ax + By + C = 0, τότε η καμπύλη έχει σχήμα ευθείας γραμμής.

Αν η εξίσωση δεύτερου βαθμού είναι, για παράδειγμα,

Ax 2 + By + C = 0 ή Ax 2 + By 2 + C = 0, τότε η καμπύλη είναι τετραγωνική, δηλ. αντιπροσωπεύει ένα από τα κωνικά τμήματα. Αυτές οι καμπύλες περιλαμβάνουν παραβολές, υπερβολές, ελλείψεις και κύκλους.

Ας απαριθμήσουμε τις γενικές μορφές εξισώσεων κωνικών τομών:

x 2 + y 2 = r 2 - κύκλος,

x 2 /a 2 + y 2 /b 2 = 1 - έλλειψη,

y = τσεκούρι 2 - παραβολή,

x 2 /a 2 – y 2 /b 2 = 1 - υπερβολή.

Καμπύλες που αντιστοιχούν στις εξισώσεις του τρίτου, τέταρτου, πέμπτου, έκτου κ.λπ. μοίρες, ονομάζονται καμπύλες της τρίτης, τέταρτης, πέμπτης, έκτης κ.λπ. Σειρά. Γενικά, όσο μεγαλύτερος είναι ο βαθμός της εξίσωσης, τόσο περισσότερες κάμψεις θα έχει η ανοιχτή καμπύλη.

Πολλές σύνθετες καμπύλες έχουν λάβει ειδικά ονόματα.

Ένα κυκλοειδές είναι μια επίπεδη καμπύλη που περιγράφεται από ένα σταθερό σημείο σε έναν κύκλο που κυλά κατά μήκος μιας ευθείας γραμμής που ονομάζεται γεννήτρια του κυκλοειδούς. ένα κυκλοειδές αποτελείται από μια σειρά επαναλαμβανόμενων τόξων.

Ένα επικυκλοειδές είναι μια επίπεδη καμπύλη που περιγράφεται από ένα σταθερό σημείο σε έναν κύκλο που κυλά σε έναν άλλο σταθερό κύκλο έξω από αυτό.

Ένα υποκυκλοειδές είναι μια επίπεδη καμπύλη που περιγράφεται από ένα σταθερό σημείο σε έναν κύκλο που κυλά από μέσα κατά μήκος ενός σταθερού κύκλου.

Μια σπείρα είναι μια επίπεδη καμπύλη που ξετυλίγεται, στροφή με τη στροφή, από ένα σταθερό σημείο (ή τυλίγεται γύρω από αυτό).

Οι μαθηματικοί μελετούν τις ιδιότητες των καμπυλών από την αρχαιότητα και τα ονόματα πολλών ασυνήθιστων καμπυλών συνδέονται με τα ονόματα εκείνων που τις μελέτησαν πρώτοι. Αυτά είναι, για παράδειγμα, η σπείρα του Αρχιμήδη, η μπούκλα Agnesi, το κισσοειδές Διοκλή, η κοχοειδής Νικομήδης και η λεμνισκάτης Bernoulli.

Στο πλαίσιο της στοιχειώδους γεωμετρίας, η έννοια της καμπύλης δεν λαμβάνει σαφή διατύπωση και μερικές φορές ορίζεται ως «μήκος χωρίς πλάτος» ή ως «το όριο ενός σχήματος». Ουσιαστικά, στη στοιχειώδη γεωμετρία, η μελέτη των καμπυλών καταλήγει στην εξέταση παραδειγμάτων (, , , και τα λοιπά.). Χωρίς γενικές μεθόδους, η στοιχειώδης γεωμετρία διείσδυσε αρκετά βαθιά στη μελέτη των ιδιοτήτων συγκεκριμένων καμπυλών (, μερικοίκαι επίσης), χρησιμοποιώντας ειδικές τεχνικές σε κάθε περίπτωση.

Τις περισσότερες φορές, μια καμπύλη ορίζεται ως μια συνεχής αντιστοίχιση από ένα τμήμα σε:

Ταυτόχρονα, οι καμπύλες μπορεί να είναι διαφορετικές, ακόμα κι αν είναιταιριάξει. Τέτοιες καμπύλες ονομάζονταιπαραμετροποιημένες καμπύλεςή αν[ ένα , σι ] = , τρόπους.

Μερικές φορές η καμπύλη καθορίζεται μέχρι , δηλαδή μέχρι την ελάχιστη σχέση ισοδυναμίας έτσι ώστε οι παραμετρικές καμπύλες

είναι ισοδύναμα αν υπάρχει συνεχής (μερικές φορές μη φθίνουσα) ηαπό το τμήμα [ ένα 1 ,σι 1 ] ανά τμήμα [ ένα 2 ,σι 2 ], έτσι ώστε

Αυτά που ορίζονται από αυτή τη σχέση ονομάζονται απλώς καμπύλες.

Αναλυτικοί ορισμοί

Στα μαθήματα αναλυτικής γεωμετρίας αποδεικνύεται ότι μεταξύ των γραμμών που είναι γραμμένες σε καρτεσιανή ορθογώνια (ή και γενική συγγένεια) συντεταγμένες με μια γενική εξίσωση δεύτερου βαθμού

Ax 2 + 2Bxy + Cy 2 + 2Dx + 2Ey + F = 0

(όπου τουλάχιστον ένας από τους συντελεστές A, B, C είναι διαφορετικός από το μηδέν) βρίσκονται μόνο οι ακόλουθοι οκτώ τύποι γραμμών:

α) έλλειψη·

β) υπερβολή.

γ) παραβολή (μη εκφυλισμένες καμπύλες δεύτερης τάξης).

δ) ένα ζεύγος τεμνόμενων γραμμών.

ε) ένα ζεύγος παράλληλων ευθειών.

στ) ένα ζεύγος γραμμών που συμπίπτουν (μία ευθεία).

ζ) ένα σημείο (εκφυλισμένες γραμμές δεύτερης τάξης).

η) μια «γραμμή» που δεν περιέχει καθόλου σημεία.

Αντίθετα, οποιαδήποτε γραμμή καθενός από τους οκτώ τύπους που υποδεικνύονται γράφεται σε καρτεσιανές ορθογώνιες συντεταγμένες με κάποια εξίσωση δεύτερης τάξης. (Στα μαθήματα αναλυτικής γεωμετρίας συνήθως μιλούν για εννέα (όχι οκτώ) τύπους κωνικών τομών, επειδή διακρίνουν μεταξύ μιας "φανταστικής έλλειψης" και ενός "ζεύγους φανταστικών παράλληλων γραμμών" - γεωμετρικά αυτές οι "γραμμές" είναι ίδιες, αφού και οι δύο κάνουν Δεν περιέχουν ένα μόνο σημείο, αλλά αναλυτικά γράφονται με διαφορετικές εξισώσεις.) Επομένως, οι κωνικές τομές (εκφυλισμένες και μη) μπορούν επίσης να οριστούν ως γραμμές δεύτερης τάξης.

ΣΕμια καμπύλη σε ένα επίπεδο ορίζεται ως ένα σύνολο σημείων των οποίων οι συντεταγμένες ικανοποιούν την εξίσωσηφά ( Χ , y ) = 0 . Ταυτόχρονα, για τη λειτουργίαφά επιβάλλονται περιορισμοί που εγγυώνται ότι αυτή η εξίσωση έχει άπειρο αριθμό αποκλίνουσες λύσεις και

αυτό το σύνολο λύσεων δεν γεμίζει το «κομμάτι του αεροπλάνου».

Αλγεβρικές καμπύλες

Μια σημαντική κατηγορία καμπυλών είναι εκείνες για τις οποίες η συνάρτησηφά ( Χ , y ) Υπάρχειαπό δύο μεταβλητές. Στην περίπτωση αυτή, η καμπύλη που ορίζεται από την εξίσωσηφά ( Χ , y ) = 0 , που ονομάζεται.

Οι αλγεβρικές καμπύλες που ορίζονται από μια εξίσωση 1ου βαθμού είναι .

Μια εξίσωση βαθμού 2, που έχει άπειρο αριθμό λύσεων, καθορίζει, δηλαδή, εκφυλισμένο και μη εκφυλισμένο.

Παραδείγματα καμπυλών που ορίζονται από εξισώσεις 3ου βαθμού: , .

Παραδείγματα καμπυλών 4ου βαθμού: και.

Παράδειγμα καμπύλης 6ου βαθμού: .

Παράδειγμα καμπύλης που ορίζεται από εξίσωση άρτιου βαθμού: (πολυεστιακή).

Οι αλγεβρικές καμπύλες που ορίζονται από εξισώσεις υψηλότερων βαθμών λαμβάνονται υπόψη. Ταυτόχρονα, η θεωρία τους γίνεται πιο αρμονική εάν η εξέταση γίνει. Στην περίπτωση αυτή, η αλγεβρική καμπύλη καθορίζεται από μια εξίσωση της μορφής

φά ( z 1 , z 2 , z 3 ) = 0 ,

Οπου φά- ένα πολυώνυμο τριών μεταβλητών που είναι σημεία.

Τύποι καμπυλών

Μια επίπεδη καμπύλη είναι μια καμπύλη στην οποία όλα τα σημεία βρίσκονται στο ίδιο επίπεδο.

(απλή γραμμή ή τόξο Ιορδάνης, επίσης περίγραμμα) - ένα σύνολο σημείων ενός επιπέδου ή χώρου που βρίσκονται σε ένα προς ένα και αμοιβαία συνεχή αντιστοιχία με ευθύγραμμα τμήματα.

Η διαδρομή είναι ένα τμήμα σε .

αναλυτικές καμπύλες που δεν είναι αλγεβρικές. Πιο συγκεκριμένα, καμπύλες που μπορούν να οριστούν μέσω της γραμμής επιπέδου μιας αναλυτικής συνάρτησης (ή, στην πολυδιάστατη περίπτωση, ενός συστήματος συναρτήσεων).

Ημιτονοειδές κύμα,

Κυκλοειδής,

Σπείρα Αρχιμήδη,

Τρακτέρ,

γραμμή αλυσίδας,

Υπερβολική σπείρα κ.λπ.

1. Μέθοδοι καθορισμού καμπυλών:

αναλυτική - η καμπύλη δίνεται από μια μαθηματική εξίσωση.

γραφικό – η καμπύλη καθορίζεται οπτικά σε έναν φορέα γραφικών πληροφοριών.

πίνακας - η καμπύλη καθορίζεται από τις συντεταγμένες μιας διαδοχικής σειράς σημείων.

παραμετρική (ο πιο συνηθισμένος τρόπος προσδιορισμού της εξίσωσης μιας καμπύλης):

Οπου - ομαλές λειτουργίες παραμέτρωνt, και

(Χ") 2 + (y") 2 + (z") 2 > 0 (συνθήκη κανονικότητας).

Είναι συχνά βολικό να χρησιμοποιείται μια αμετάβλητη και συμπαγής αναπαράσταση της εξίσωσης μιας καμπύλης χρησιμοποιώντας:

όπου στην αριστερή πλευρά υπάρχουν σημεία της καμπύλης, και η δεξιά πλευρά καθορίζει την εξάρτησή της από κάποια παράμετρο t. Επεκτείνοντας αυτήν την καταχώρηση σε συντεταγμένες, λαμβάνουμε τον τύπο (1).

1. Κυκλοειδής.

Η ιστορία της μελέτης του κυκλοειδούς συνδέεται με τα ονόματα τόσο μεγάλων επιστημόνων, φιλοσόφων, μαθηματικών και φυσικών όπως ο Αριστοτέλης, ο Πτολεμαίος, ο Γαλιλαίος, ο Huygens, ο Torricelli και άλλοι.

Κυκλοειδής(απόκυκλοειδής - στρογγυλό) -, το οποίο μπορεί να οριστεί ως η τροχιά ενός σημείου που βρίσκεται στο όριο ενός κύκλου που κυλά χωρίς να ολισθαίνει σε ευθεία γραμμή. Αυτός ο κύκλος ονομάζεται δημιουργία.

Μία από τις παλαιότερες μεθόδους σχηματισμού καμπυλών είναι η κινηματική μέθοδος, στην οποία η καμπύλη προκύπτει ως η τροχιά ενός σημείου. Μια καμπύλη που λαμβάνεται ως η τροχιά ενός σημείου στερεωμένο σε έναν κύκλο, που κυλά χωρίς να ολισθαίνει κατά μήκος μιας ευθείας γραμμής, κατά μήκος ενός κύκλου ή άλλης καμπύλης, ονομάζεται κυκλοειδές, που μεταφράζεται από τα ελληνικά σημαίνει κυκλικό, που θυμίζει κύκλο.

Ας εξετάσουμε πρώτα την περίπτωση όταν ο κύκλος κυλά κατά μήκος μιας ευθείας γραμμής. Η καμπύλη που περιγράφεται από ένα σημείο στερεωμένο σε έναν κύκλο που κυλά χωρίς να ολισθαίνει σε ευθεία γραμμή ονομάζεται κυκλοειδές.

Αφήστε έναν κύκλο ακτίνας R να κυλήσει κατά μήκος μιας ευθείας γραμμής a. Το C είναι ένα σημείο στερεωμένο σε έναν κύκλο, την αρχική χρονική στιγμή που βρίσκεται στη θέση Α (Εικ. 1). Ας σχεδιάσουμε στη γραμμή a ένα τμήμα ΑΒ ίσο με το μήκος του κύκλου, δηλ. AB = 2 π R. Διαιρέστε αυτό το τμήμα σε 8 ίσα μέρη με τα σημεία A1, A2, ..., A8 = B.

Είναι σαφές ότι όταν ο κύκλος, κυλιόμενος κατά μήκος της ευθείας α, κάνει μία περιστροφή, δηλ. περιστρέφεται 360, τότε θα πάρει τη θέση (8) και το σημείο C θα μετακινηθεί από τη θέση Α στη θέση Β.

Αν ο κύκλος κάνει μισή πλήρη περιστροφή, δηλ. στρίβει 180, τότε θα πάρει τη θέση (4) και το σημείο C θα μετακινηθεί στην υψηλότερη θέση C4.

Εάν ο κύκλος περιστρέφεται κατά γωνία 45, ο κύκλος θα μετακινηθεί στη θέση (1) και το σημείο C θα μετακινηθεί στη θέση C1.

Το σχήμα 1 δείχνει επίσης άλλα σημεία του κυκλοειδούς που αντιστοιχούν στις υπόλοιπες γωνίες περιστροφής του κύκλου, πολλαπλάσια του 45.

Συνδέοντας τα κατασκευασμένα σημεία με μια ομαλή καμπύλη, παίρνουμε ένα τμήμα του κυκλοειδούς που αντιστοιχεί σε μια πλήρη περιστροφή του κύκλου. Στις επόμενες στροφές θα ληφθούν τα ίδια τμήματα, δηλ. Το κυκλοειδές θα αποτελείται από ένα περιοδικά επαναλαμβανόμενο τμήμα που ονομάζεται τόξο του κυκλοειδούς.

Ας προσέξουμε τη θέση της εφαπτομένης στο κυκλοειδές (Εικ. 2). Εάν ένας ποδηλάτης οδηγεί σε βρεγμένο δρόμο, τότε οι σταγόνες που βγαίνουν από τον τροχό θα πετάξουν εφαπτομενικά στον κυκλοειδή και, ελλείψει ασπίδων, μπορούν να πιτσιλίσουν την πλάτη του ποδηλάτη.

Ο πρώτος άνθρωπος που μελέτησε το κυκλοειδές ήταν ο Galileo Galilei (1564 – 1642). Βρήκε και το όνομά του.

Ιδιότητες του κυκλοειδούς:

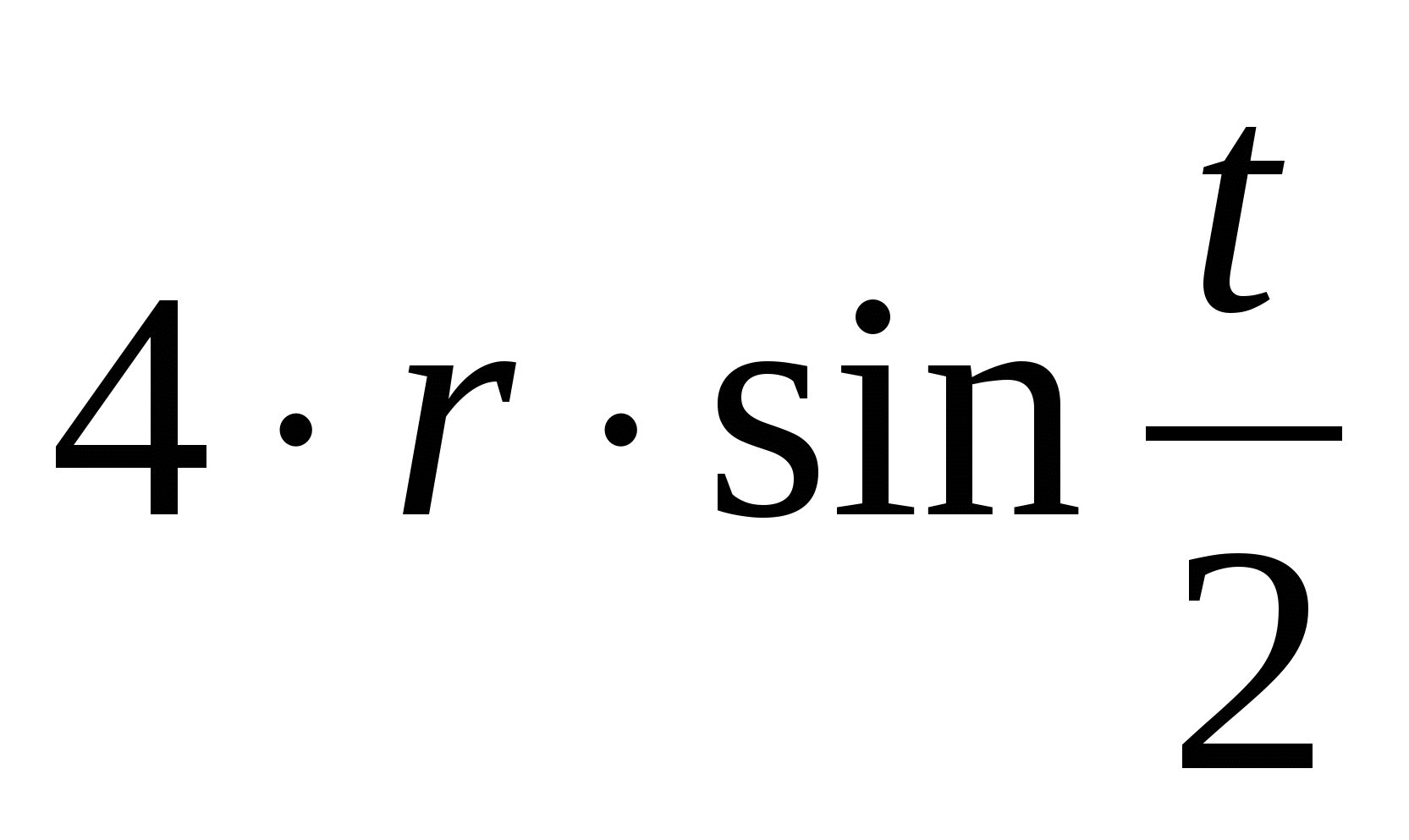
Το Cycloid έχει μια σειρά από αξιόλογες ιδιότητες. Ας αναφέρουμε μερικά από αυτά.

Ιδιοκτησία 1. (Παγωμένο βουνό.) Το 1696, ο I. Bernoulli έθεσε το πρόβλημα της εύρεσης της καμπύλης της πιο απότομης καθόδου, ή, με άλλα λόγια, το πρόβλημα του σχήματος μιας παγοτσουλήθρας για να την κυλήσει προς τα κάτω για να κάνει το ταξίδι από το σημείο εκκίνησης Α έως το σημείο λήξης Β στο συντομότερο χρονικό διάστημα (Εικ. 3, α). Η επιθυμητή καμπύλη ονομάστηκε «βραχιστόχρονος», δηλ. καμπύλη συντομότερου χρόνου.

Είναι σαφές ότι η συντομότερη διαδρομή από το σημείο Α στο σημείο Β είναι το τμήμα ΑΒ. Ωστόσο, με μια τέτοια ευθύγραμμη κίνηση, η ταχύτητα αυξάνεται αργά και ο χρόνος που αφιερώνεται στην κάθοδο αποδεικνύεται μεγάλος (Εικ. 3, β).

Όσο πιο απότομη είναι η κατάβαση, τόσο πιο γρήγορα αυξάνεται η ταχύτητα. Ωστόσο, με μια απότομη κατηφόρα, η διαδρομή κατά μήκος της καμπύλης επιμηκύνεται και ως εκ τούτου αυξάνει τον χρόνο που απαιτείται για την ολοκλήρωσή της.

Μεταξύ των μαθηματικών που έλυσαν αυτό το πρόβλημα ήταν οι: G. Leibniz, I. Newton, G. L'Hopital και J. Bernoulli. Απέδειξαν ότι η επιθυμητή καμπύλη είναι ένα ανεστραμμένο κυκλοειδές (Εικ. 3, α). Οι μέθοδοι που αναπτύχθηκαν από αυτούς τους επιστήμονες για την επίλυση του προβλήματος του βραχιστόχρονου έθεσαν τα θεμέλια για μια νέα κατεύθυνση στα μαθηματικά - τον λογισμό των παραλλαγών.

Ιδιοκτησία 2. (Ρολόι με εκκρεμές.) Ένα ρολόι με συνηθισμένο εκκρεμές δεν μπορεί να τρέξει με ακρίβεια, αφού η περίοδος ταλάντωσης ενός εκκρεμούς εξαρτάται από το πλάτος του: όσο μεγαλύτερο είναι το πλάτος, τόσο μεγαλύτερη η περίοδος. Ο Ολλανδός επιστήμονας Christiaan Huygens (1629 – 1695) αναρωτήθηκε τι καμπύλη πρέπει να ακολουθεί μια μπάλα στη χορδή ενός εκκρεμούς ώστε η περίοδος των ταλαντώσεων της να μην εξαρτάται από το πλάτος. Σημειώστε ότι σε ένα συνηθισμένο εκκρεμές, η καμπύλη κατά μήκος της οποίας κινείται η μπάλα είναι ένας κύκλος (Εικ. 4).

Η καμπύλη που αναζητούσαμε αποδείχθηκε ότι ήταν ένα ανεστραμμένο κυκλοειδές. Εάν, για παράδειγμα, μια τάφρο είναι φτιαγμένη σε σχήμα ανεστραμμένου κυκλοειδούς και μια μπάλα εκτοξεύεται κατά μήκος της, τότε η περίοδος κίνησης της μπάλας υπό την επίδραση της βαρύτητας δεν θα εξαρτάται από την αρχική της θέση και πλάτος (Εικ. 5 ). Για αυτήν την ιδιότητα, το κυκλοειδές ονομάζεται επίσης "ταυτοχρόνιο" - μια καμπύλη ίσων χρόνων.

Ο Huygens έφτιαξε δύο ξύλινες σανίδες με άκρες σε σχήμα κυκλοειδούς, περιορίζοντας την κίνηση του νήματος αριστερά και δεξιά (Εικ. 6). Σε αυτή την περίπτωση, η ίδια η μπάλα θα κινηθεί κατά μήκος ενός ανεστραμμένου κυκλοειδούς και, επομένως, η περίοδος των ταλαντώσεων της δεν θα εξαρτάται από το πλάτος.

Από αυτή την ιδιότητα του κυκλοειδούς, συγκεκριμένα, προκύπτει ότι ανεξάρτητα από το σημείο του πάγου σε σχήμα ανεστραμμένου κυκλοειδούς αρχίζουμε την κάθοδό μας, θα περάσουμε τον ίδιο χρόνο μέχρι το τελικό σημείο.

Κυκλοειδής εξίσωση

1. Είναι βολικό να γράψετε την κυκλική εξίσωση ως α - η γωνία περιστροφής του κύκλου, εκφρασμένη σε ακτίνια, σημειώστε ότι το α είναι επίσης ίσο με τη διαδρομή που διανύει ο κύκλος παραγωγής σε ευθεία γραμμή.

x=rα– rαμαρτία α

y=r – r cos α

2. Ας πάρουμε τον οριζόντιο άξονα συντεταγμένων ως την ευθεία γραμμή κατά μήκος της οποίας κυλά ο κύκλος δημιουργίας της ακτίνας r.

Το κυκλοειδές περιγράφεται με παραμετρικές εξισώσεις

Χ = rt – rαμαρτία t,

y = r – r cos t.

Εξίσωση σε:

Το κυκλοειδές μπορεί να ληφθεί λύνοντας τη διαφορική εξίσωση:

Από την ιστορία του κυκλοειδούς

Ο πρώτος επιστήμονας που έδωσε προσοχή στο κυκλοειδέςV, αλλά η σοβαρή έρευνα σε αυτήν την καμπύλη ξεκίνησε μόλις το.

Ο πρώτος άνθρωπος που μελέτησε το κυκλοειδές ήταν ο Galileo Galilei (1564-1642), ο διάσημος Ιταλός αστρονόμος, φυσικός και εκπαιδευτικός. Βρήκε επίσης το όνομα «κυκλοειδές», που σημαίνει «θυμίζει κύκλο». Ο ίδιος ο Γαλιλαίος δεν έγραψε τίποτα για τον κυκλοειδή, αλλά το έργο του προς αυτή την κατεύθυνση αναφέρεται από τους μαθητές και τους οπαδούς του Γαλιλαίου: Viviani, Toricelli και άλλοι. Ο Τοριτσέλι, διάσημος φυσικός και εφευρέτης του βαρόμετρου, αφιέρωσε πολύ χρόνο στα μαθηματικά. Κατά τη διάρκεια της Αναγέννησης δεν υπήρχαν στενοί ειδικοί επιστήμονες. Ένας ταλαντούχος άνθρωπος σπούδασε φιλοσοφία, φυσική και μαθηματικά και παντού έλαβε ενδιαφέροντα αποτελέσματα και έκανε σημαντικές ανακαλύψεις. Λίγο αργότερα από τους Ιταλούς, οι Γάλλοι πήραν το κυκλοειδές, αποκαλώντας το "ρουλέτα" ή "τροχοειδές". Το 1634, ο Roberval - ο εφευρέτης του περίφημου συστήματος ζυγών - υπολόγισε την περιοχή που οριοθετείται από το τόξο ενός κυκλοειδούς και τη βάση του. Μια ουσιαστική μελέτη του κυκλοειδούς πραγματοποιήθηκε από έναν σύγχρονο του Γαλιλαίου. Μεταξύ , δηλαδή, καμπυλών των οποίων η εξίσωση δεν μπορεί να γραφτεί με τη μορφή Χ , y, το κυκλοειδές είναι το πρώτο από αυτά που μελετήθηκαν.

Έγραψε για το κυκλοειδές:

Η ρουλέτα είναι μια γραμμή τόσο κοινή που μετά την ευθεία γραμμή και τον κύκλο δεν υπάρχει γραμμή που συναντάται πιο συχνά. σκιαγραφείται τόσο συχνά μπροστά στα μάτια όλων, που πρέπει να εκπλαγεί κανείς που οι αρχαίοι δεν το θεωρούσαν... γιατί δεν είναι τίποτα άλλο από ένα μονοπάτι που περιγράφεται στον αέρα με το καρφί ενός τροχού.

Η νέα καμπύλη κέρδισε γρήγορα δημοτικότητα και υποβλήθηκε σε εις βάθος ανάλυση, η οποία περιελάμβανε, , Νεύτωνας,, οι αδερφοί Μπερνούλι και άλλοι διαφωτιστές της επιστήμης του 17ου-18ου αιώνα. Στο κυκλοειδές, οι μέθοδοι που εμφανίστηκαν εκείνα τα χρόνια ακονίστηκαν ενεργά. Το γεγονός ότι η αναλυτική μελέτη του κυκλοειδούς αποδείχθηκε εξίσου επιτυχημένη με την ανάλυση των αλγεβρικών καμπυλών έκανε μεγάλη εντύπωση και έγινε ένα σημαντικό επιχείρημα υπέρ των «ίσων δικαιωμάτων» των αλγεβρικών και υπερβατικών καμπυλών. Επικυκλοειδές

Μερικοί τύποι κυκλοειδών

Επικυκλοειδές - η τροχιά του σημείου Α, που βρίσκεται σε έναν κύκλο διαμέτρου D, ο οποίος κυλά χωρίς να ολισθαίνει κατά μήκος ενός οδηγού κύκλου ακτίνας R (εξωτερική επαφή).

Η κατασκευή του επικυκλοειδούς πραγματοποιείται με την ακόλουθη σειρά:

Από το κέντρο 0, σχεδιάστε ένα βοηθητικό τόξο με ακτίνα ίση με 000=R+r.

Από τα σημεία 01, 02, ...012, ως από κέντρα, σχεδιάστε κύκλους ακτίνας r μέχρι να τέμνονται με βοηθητικά τόξα στα σημεία Α1, Α2, ... Α12, που ανήκουν στο επικυκλοειδές.

Υποκυκλοειδές

Υποκυκλοειδές είναι η τροχιά του σημείου Α που βρίσκεται σε έναν κύκλο διαμέτρου D, ο οποίος κυλίεται χωρίς να ολισθαίνει κατά μήκος ενός οδηγού κύκλου ακτίνας R (εσωτερική εφαπτομένη).

Η κατασκευή ενός υποκυκλοειδούς πραγματοποιείται με την ακόλουθη σειρά:

Ο κύκλος δημιουργίας ακτίνας r και ο κατευθυντικός κύκλος ακτίνας R σχεδιάζονται έτσι ώστε να εφάπτονται στο σημείο Α.

Ο κύκλος παραγωγής χωρίζεται σε 12 ίσα μέρη, λαμβάνονται τα σημεία 1, 2, ... 12.

Από το κέντρο 0, σχεδιάστε ένα βοηθητικό τόξο με ακτίνα ίση με 000=R-r.

Η κεντρική γωνία a καθορίζεται από τον τύπο a =360r/R.

Διαιρέστε το τόξο του οδηγού κύκλου, που περιορίζεται από τη γωνία α, σε 12 ίσα μέρη, λαμβάνοντας τα σημεία 11, 21, ...121.

Από το κέντρο 0, χαράσσονται ευθείες γραμμές μέσω των σημείων 11, 21, ...121 έως ότου τέμνονται με το βοηθητικό τόξο στα σημεία 01, 02, ...012.

Από το κέντρο 0, τα βοηθητικά τόξα σχεδιάζονται μέσω των σημείων διαίρεσης 1, 2, ... 12 του κύκλου δημιουργίας.

Από τα σημεία 01, 02, ...012, ως από κέντρα, σχεδιάστε κύκλους ακτίνας r μέχρι να τέμνονται με βοηθητικά τόξα στα σημεία Α1, Α2, ... Α12, που ανήκουν στο υποκυκλοειδές.

1. Καρδιοειδές.

Καρδιοειδές ( καρδία - καρδιά, Το καρδιοειδές είναι μια ειδική περίπτωση Ο όρος "καρδιοειδές" εισήχθη από τον Castillon το 1741.

Αν πάρουμε έναν κύκλο και ένα σημείο πάνω του ως πόλο, θα λάβουμε ένα καρδιοειδές μόνο αν σχεδιάσουμε τμήματα ίσα με τη διάμετρο του κύκλου. Για άλλα μεγέθη εναποτιθέμενων τμημάτων, τα κονχοειδή θα είναι επιμήκη ή κοντύτερα καρδιοειδή. Αυτά τα επιμήκη και βραχυνεμένα καρδιοειδή ονομάζονται αλλιώς κοχλίας του Pascal.

Το Cardioid έχει διάφορες εφαρμογές στην τεχνολογία. Τα καρδιοειδή σχήματα χρησιμοποιούνται για την κατασκευή εκκεντρικών και έκκεντρων για αυτοκίνητα. Μερικές φορές χρησιμοποιείται όταν σχεδιάζετε γρανάζια. Επιπλέον, χρησιμοποιείται στην οπτική τεχνολογία.

Ιδιότητες ενός καρδιοειδούς

Καρδιοειδές -Το B M σε έναν κινούμενο κύκλο θα περιγράφει μια κλειστή τροχιά. Αυτή η επίπεδη καμπύλη ονομάζεται καρδιοειδές.

2) Το καρδιοειδές μπορεί να ληφθεί με άλλο τρόπο. Σημειώστε ένα σημείο στον κύκλο ΣΧΕΤΙΚΑ ΜΕκαι ας τραβήξουμε ένα δοκάρι από αυτό. Αν από σημείο ΕΝΑτομή αυτής της ακτίνας με έναν κύκλο, σχεδιάστε ένα τμήμα ΕΙΜΑΙ,μήκος ίσο με τη διάμετρο του κύκλου και η ακτίνα περιστρέφεται γύρω από το σημείο ΣΧΕΤΙΚΑ ΜΕ, μετά το σημείο Μθα κινηθεί κατά μήκος του καρδιοειδούς.

3) Ένα καρδιοειδές μπορεί επίσης να αναπαρασταθεί ως καμπύλη εφαπτομένη σε όλους τους κύκλους που έχουν κέντρα σε έναν δεδομένο κύκλο και διέρχονται από το σταθερό σημείο του. Όταν κατασκευάζονται αρκετοί κύκλοι, το καρδιοειδές φαίνεται να είναι κατασκευασμένο σαν από μόνο του.

4) Υπάρχει επίσης ένας εξίσου κομψός και απροσδόκητος τρόπος για να δείτε το καρδιοειδές. Στο σχήμα μπορείτε να δείτε μια σημειακή πηγή φωτός σε έναν κύκλο. Αφού οι φωτεινές ακτίνες αντανακληθούν για πρώτη φορά από τον κύκλο, ταξιδεύουν εφαπτομενικά στο καρδιοειδές. Φανταστείτε τώρα ότι ο κύκλος είναι οι άκρες ενός φλιτζανιού αντανακλάται σε ένα σημείο ένας λαμπερός λαμπτήρας. Ο μαύρος καφές χύνεται στο φλιτζάνι, επιτρέποντάς σας να δείτε τις φωτεινές ανακλώμενες ακτίνες. Ως αποτέλεσμα, το καρδιοειδές τονίζεται από ακτίνες φωτός.

1. Αστροειδής.

Αστροειδής (από το ελληνικό άστρο - αστέρι και είδος - άποψη), μια επίπεδη καμπύλη που περιγράφεται από ένα σημείο σε κύκλο που εφάπτεται από το εσωτερικό ενός σταθερού κύκλου τετραπλάσιας της ακτίνας και κυλίεται κατά μήκος του χωρίς να γλιστράει. Ανήκει στα υποκυκλοειδή. Το Astroid είναι μια αλγεβρική καμπύλη 6ης τάξης.

Αστροειδής.

Το μήκος ολόκληρου του αστροειδούς είναι ίσο με τις έξι ακτίνες του σταθερού κύκλου και η περιοχή που περιορίζεται από αυτό είναι τα τρία όγδοα του σταθερού κύκλου.

Το εφαπτόμενο τμήμα στο αστροειδές, που περικλείεται ανάμεσα σε δύο αμοιβαία κάθετες ακτίνες του σταθερού κύκλου που σχεδιάζονται στις άκρες του αστεροειδή, είναι ίσο με την ακτίνα του σταθερού κύκλου, ανεξάρτητα από το πώς επιλέχθηκε το σημείο.

Ιδιότητες του αστροειδούς

Υπάρχουν τέσσερακάσπα .

Μήκος τόξου από το σημείο 0 έως τον φάκελο

οικογένειες τμημάτων σταθερού μήκους, τα άκρα των οποίων βρίσκονται σε δύο αμοιβαία κάθετες γραμμές.

Το Astroid είναι 6ης τάξης.

Αστροειδείς εξισώσεις

Εξίσωση σε καρτεσιανές ορθογώνιες συντεταγμένες:| x | 2 / 3 + | y | 2 / 3 = R 2 / 3παραμετρική εξίσωση:x = Rcos 3 t y = Rsin 3 t

Μέθοδος για την κατασκευή ενός αστεροειδή

Σχεδιάζουμε δύο αμοιβαία κάθετες ευθείες γραμμές και σχεδιάζουμε μια σειρά από τμήματα μήκουςR , του οποίου τα άκρα βρίσκονται σε αυτές τις γραμμές. Το σχήμα δείχνει 12 τέτοια τμήματα (συμπεριλαμβανομένων τμημάτων των ίδιων των αμοιβαία κάθετων ευθειών). Όσο περισσότερα τμήματα σχεδιάζουμε, τόσο πιο ακριβής θα έχουμε την καμπύλη. Ας κατασκευάσουμε τώρα το περίβλημα όλων αυτών των τμημάτων. Αυτός ο φάκελος θα είναι το astroid.

1. συμπέρασμα

Η εργασία παρέχει παραδείγματα προβλημάτων με διαφορετικούς τύπους καμπυλών, που ορίζονται από διαφορετικές εξισώσεις ή ικανοποιούν κάποια μαθηματική συνθήκη. Συγκεκριμένα, κυκλοειδείς καμπύλες, μέθοδοι ορισμού τους, διάφορες μέθοδοι κατασκευής, ιδιότητες αυτών των καμπυλών.

Οι ιδιότητες των κυκλοειδών καμπυλών χρησιμοποιούνται πολύ συχνά στη μηχανική σε γρανάζια, γεγονός που αυξάνει σημαντικά την αντοχή των εξαρτημάτων στους μηχανισμούς.

Το Cyclomis (από το ελληνικό khklpeidYut - στρογγυλό) είναι μια επίπεδη υπερβατική καμπύλη. Ένα κυκλοειδές ορίζεται κινηματικά ως η τροχιά ενός σταθερού σημείου ενός κύκλου παραγωγής ακτίνας r, που κυλίεται χωρίς να ολισθαίνει σε ευθεία γραμμή.

Εξισώσεις

Ας πάρουμε τον οριζόντιο άξονα συντεταγμένων ως την ευθεία γραμμή κατά μήκος της οποίας κυλάει ο κύκλος δημιουργίας της ακτίνας r.

· Το κυκλοειδές περιγράφεται με παραμετρικές εξισώσεις

Εξίσωση σε καρτεσιανές συντεταγμένες:

· Το κυκλοειδές μπορεί να ληφθεί ως λύση στη διαφορική εξίσωση:

Ιδιότητες

• · Κυκλοειδής --περιοδική συνάρτηση κατά μήκος του άξονα x, με περίοδο 2ρr. Είναι βολικό να λαμβάνουμε ενικά σημεία (σημεία επιστροφής) της μορφής t = 2рk, όπου το k είναι ένας αυθαίρετος ακέραιος, ως όρια της περιόδου.
• · Για να σχεδιάσουμε μια εφαπτομένη σε ένα κυκλοειδές σε ένα αυθαίρετο σημείο Α, αρκεί να συνδέσουμε αυτό το σημείο με το πάνω σημείο του κύκλου παραγωγής. Συνδέοντας το Α στο κάτω σημείο του κύκλου παραγωγής, παίρνουμε το κανονικό.
• · Το μήκος του κυκλοειδούς τόξου είναι 8r. Αυτή η ιδιοκτησία ανακαλύφθηκε από τον Christopher Wren (1658).
• · Η περιοχή κάτω από κάθε τόξο του κυκλοειδούς είναι τρεις φορές μεγαλύτερη από την περιοχή του κύκλου παραγωγής. Ο Torricelli ισχυρίζεται ότι αυτό το γεγονός ανακαλύφθηκε από τον Galileo.
• · Η ακτίνα καμπυλότητας του πρώτου τόξου του κυκλοειδούς είναι ίση.

• · Το «ανεστραμμένο» κυκλοειδές είναι μια καμπύλη με την πιο απότομη κάθοδο (βραχιστόχρονο). Επιπλέον, έχει επίσης την ιδιότητα της ταυτόχρονης: ένα βαρύ σώμα τοποθετημένο σε οποιοδήποτε σημείο του κυκλοειδούς τόξου φτάνει ταυτόχρονα στην οριζόντια.
• · Η περίοδος ταλάντωσης ενός υλικού σημείου που ολισθαίνει κατά μήκος ενός ανεστραμμένου κυκλοειδούς δεν εξαρτάται από το πλάτος αυτό το γεγονός χρησιμοποιήθηκε από τον Huygens για να δημιουργήσει ένα ακριβές μηχανικό ρολόι.
• · Η εξέλιξη ενός κυκλοειδούς είναι ένα κυκλοειδές σύμφωνο με το αρχικό, δηλαδή, παράλληλη μετατόπιση έτσι ώστε οι κορυφές να μετατραπούν σε «σημεία».
• · Τα μέρη της μηχανής που εκτελούν ταυτόχρονα ομοιόμορφη περιστροφική και μεταφορική κίνηση περιγράφουν κυκλοειδείς καμπύλες (κυκλοειδές, επικυκλοειδές, υποκυκλοειδές, τροχοειδές, αστροειδής) (πρβλ. κατασκευή του λημνιστικού του Bernoulli).