Maksimums- og minimumsfunksjoner er eksempler på løsninger. Hva er ekstrema for en funksjon: kritiske punkter for maksimum og minimum. Nødvendig betingelse for ytterpunktet av en funksjon

Funksjonsverdier og maksimums- og minimumspoeng

Største funksjonsverdi

Minste funksjonsverdi

Som gudfaren sa: "Ikke noe personlig." Bare derivater!

Statistikkoppgave 12 anses som ganske vanskelig, og alt fordi gutta ikke leste denne artikkelen (vits). I de fleste tilfeller er uforsiktighet skylden.

12 oppgave er av to typer:

1. Finn maksimums-/minimumspunktet (be om å finne "x"-verdiene).
2. Finn den største/minste verdien av en funksjon (be om å finne "y"-verdiene).

Hvordan opptre i disse tilfellene?

Finn maksimums-/minimumspunktet

1. Lik det til null.
2. "x" funnet eller funnet vil være minimum eller maksimum poeng.
3. Bestem tegnene ved hjelp av intervallmetoden og velg hvilket punkt som er nødvendig i oppgaven.

Unified State Examination oppgaver:

Finn maksimumspunktet for funksjonen

• Vi tar den deriverte:

Det stemmer, først øker funksjonen, deretter reduseres - dette er maksimumspunktet!
Svar: −15

Finn minimumspunktet for funksjonen

• La oss transformere og ta den deriverte:

• Flott! Først reduseres funksjonen, så øker - dette er minimumspunktet!

Svar: −2

Finn den største/minste verdien av en funksjon

1. Ta den deriverte av den foreslåtte funksjonen.
   
2. Lik det til null.
   
3. Den funnet "x" vil være minimums- eller maksimumspunktet.
   
4. Bestem tegnene ved hjelp av intervallmetoden og velg hvilket punkt som er nødvendig i oppgaven.
5. I slike oppgaver er det alltid spesifisert et gap: X-ene funnet i trinn 3 må inkluderes i dette gapet.
6. Bytt inn det resulterende maksimums- eller minimumspunktet i den opprinnelige ligningen, og vi får den største eller minste verdien av funksjonen.

Unified State Examination oppgaver:

Finn den største verdien av funksjonen på intervallet [−4; −1]

Svar: −6

Finn den største verdien av funksjonen på segmentet

• Maksimumsverdien for funksjonen er "11" ved maksimumspunktet (på dette segmentet) "0".

Svar: 11

Konklusjoner:

1. 70 % av feilene er at gutter ikke husker hva som svar på den største/minste verdien av funksjonen skal skrives "y", og på skriv maksimums-/minimumspunktet "x".
2. Finnes det ingen løsning på den deriverte når man skal finne verdiene til en funksjon? Ikke noe problem, bytt ut de ekstreme punktene i gapet!
3. Svaret kan alltid skrives som et tall eller en desimal. Nei? Tenk deretter eksemplet på nytt.
4. I de fleste oppgaver vil vi få ett poeng og vår latskap med å sjekke maksimum eller minimum vil være berettiget. Vi har ett poeng - du kan trygt skrive tilbake.
5. Og her Du bør ikke gjøre dette når du søker etter verdien av en funksjon! Sjekk at dette er det rette punktet, ellers kan de ekstreme verdiene av gapet være større eller mindre.

En enkel algoritme for å finne ekstreme..

• Finne den deriverte av funksjonen
• Vi likestiller denne deriverte til null
• Vi finner verdiene til variabelen til det resulterende uttrykket (verdiene til variabelen der den deriverte konverteres til null)
• Ved å bruke disse verdiene deler vi koordinatlinjen i intervaller (ikke glem bruddpunktene, som også må plottes på linjen), alle disse punktene kalles "mistenkelige" punkter for ekstremumet
• Vi beregner hvilke av disse intervallene den deriverte vil være positiv og hvilke som vil være negativ. For å gjøre dette, må du erstatte verdien fra intervallet i den deriverte.

Av punktene som er mistenkelige for et ekstremum, er det nødvendig å finne . For å gjøre dette ser vi på intervallene våre på koordinatlinjen. Hvis fortegnet for den deriverte endres fra pluss til minus når du passerer gjennom et punkt, vil dette punktet være maksimum, og hvis fra minus til pluss, da minimum.

For å finne de største og minste verdiene til en funksjon, må du beregne verdien av funksjonen i enden av segmentet og ved ytterpunktene. Velg deretter den største og minste verdien.

La oss se på et eksempel
Finn den deriverte og lig den med null:

Vi plotter de oppnådde verdiene til variablene på koordinatlinjen og beregner tegnet til den deriverte på hvert av intervallene. Vel, for eksempel, for den første la oss ta-2 , da vil den deriverte være lik-0,24 , for det andre tar vi0 , da blir den deriverte2 , og for den tredje tar vi2 , da blir den deriverte-0,24. Vi setter ned de passende skiltene.

Vi ser at når den passerer gjennom punkt -1, endrer den deriverte fortegn fra minus til pluss, det vil si at dette vil være minimumspunktet, og når den passerer gjennom 1, vil den skifte fortegn fra henholdsvis pluss til minus, dette vil være maksimum poeng.

Teorem. (en nødvendig betingelse for eksistensen av et ekstremum) Hvis funksjonen f(x) er differensierbar i punktet x = x 1 og punktet x 1 er et ekstremumpunkt, forsvinner den deriverte av funksjonen på dette punktet.

Bevis. La oss anta at funksjonen f(x) har et maksimum i punktet x = x 1.

Så for tilstrekkelig liten positiv Dх>0 er følgende ulikhet sann:

A-priory:

De. hvis Dх®0, men Dх<0, то f¢(x 1) ³ 0, а если Dх®0, но Dх>0, deretter f¢(x 1) £ 0.

Og dette er bare mulig hvis ved Dх®0 f¢(x 1) = 0.

For tilfellet hvis funksjonen f(x) har et minimum ved punkt x 2, bevises teoremet på lignende måte.

Teoremet er bevist.

Konsekvens. Det motsatte utsagnet er ikke sant. Hvis den deriverte av en funksjon på et bestemt punkt er lik null, betyr ikke dette at funksjonen har et ekstremum på dette punktet. Et veltalende eksempel på dette er funksjonen y = x 3, hvis deriverte i punktet x = 0 er lik null, men på dette punktet har funksjonen bare en bøyning, og ikke et maksimum eller minimum.

Definisjon. Kritiske punkter funksjoner er punktene der den deriverte av funksjonen ikke eksisterer eller er lik null.

Teoremet diskutert ovenfor gir oss de nødvendige betingelsene for eksistensen av et ekstremum, men dette er ikke nok.

Eksempel: f(x) = ôxô Eksempel: f(x) =

y y

Ved punktet x = 0 har funksjonen et minimum, men i punktet x = 0 har funksjonen ingen av delene

har ingen derivater. maksimum, ingen minimum, ingen produksjon

Generelt sett kan funksjonen f(x) ha et ekstremum på punkter der den deriverte ikke eksisterer eller er lik null.

Teorem. (Tilstrekkelige forhold for eksistensen av et ekstremum)

La funksjonen f(x) være kontinuerlig i intervallet (a, b), som inneholder det kritiske punktet x 1, og differensierbar på alle punkter i dette intervallet (unntatt kanskje selve punktet x 1).

Hvis, når den går gjennom punktet x 1 fra venstre til høyre, den deriverte av funksjonen f¢(x) endrer fortegn fra “+” til “-“, så har funksjonen f(x) ved punktet x = x 1 et maksimum, og hvis den deriverte endrer fortegn fra "- " til "+" - så har funksjonen et minimum.

Bevis.

La

I følge Lagranges teorem: f(x) – f(x 1) = f¢(e)(x – x 1), hvor x< e < x 1 .

Deretter: 1) Hvis x< x 1 , то e < x 1 ; f¢(e)>0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x 1)<0 или f(x) < f(x 1).

2) Hvis x > x 1, så e > x 1 f¢(e)<0; f¢(e)(x – x 1)<0, следовательно

f(x) – f(x 1)<0 или f(x) < f(x 1).

Siden svarene er sammenfallende, kan vi si at f(x)< f(x 1) в любых точках вблизи х 1 , т.е. х 1 – точка максимума.

Beviset for teoremet for minimumspoeng er likt.

Teoremet er bevist.

Basert på ovenstående kan du utvikle en enhetlig prosedyre for å finne de største og minste verdiene av en funksjon på et segment:

1) Finn de kritiske punktene til funksjonen.

2) Finn verdiene til funksjonen på kritiske punkter.

3) Finn verdiene til funksjonen i enden av segmentet.

4) Velg den største og minste blant de oppnådde verdiene.

Studerer en funksjon for et ekstremum ved hjelp av

derivater av høyere orden.

La ved punktet x = x 1 f¢(x 1) = 0 og f¢¢(x 1) eksisterer og er kontinuerlig i et eller annet nærområde til punktet x 1.

Teorem. Hvis f¢(x 1) = 0, så har funksjonen f(x) i punktet x = x 1 et maksimum hvis f¢¢(x 1)<0 и минимум, если f¢¢(x 1)>0.

Bevis.

La f¢(x 1) = 0 og f¢¢(x 1)<0. Т.к. функция f(x) непрерывна, то f¢¢(x 1) будет отрицательной и в некоторой малой окрестности точки х 1 .

Fordi f¢¢(x) = (f¢(x))¢< 0, то f¢(x) убывает на отрезке, содержащем точку х 1 , но f¢(x 1)=0, т.е. f¢(x) >0 på x x 1. Dette betyr at når den passerer gjennom punktet x = x 1, endrer den deriverte f¢(x) fortegn fra “+” til “-“, dvs.

på dette tidspunktet har funksjonen f(x) et maksimum.

For tilfellet med en minimumsfunksjon, er teoremet bevist på lignende måte.

Hvis f¢¢(x) = 0, er arten av det kritiske punktet ukjent. Ytterligere forskning er nødvendig for å fastslå det.

Konveksitet og konkavitet av en kurve.

Bøyningspunkter.

Definisjon. Kurven er konveks opp på intervallet (a, b) hvis alle punktene ligger under noen av tangentene på dette intervallet. En kurve konveks oppover kalles konveks, og en kurve som vender konvekst nedover kalles konkav.

på

Figuren viser en illustrasjon av definisjonen ovenfor.

Teorem 1. Hvis på alle punkter i intervallet (a, b) den andrederiverte av funksjonen f(x) er negativ, så er kurven y = f(x) konveks oppover (konveks).

Bevis. La x 0 О (a, b). La oss tegne en tangent til kurven på dette punktet.

Kurveligning: y = f(x);

Tangentligning:

Det må bevises.

Ved Lagranges teorem for f(x) – f(x 0): , x 0< c < x.

I følge Lagranges teorem for

La x > x 0 og deretter x 0< c 1 < c < x. Т.к. x – x 0 >0 og c – x 0 > 0, og i tillegg etter tilstand

Derfor,.

La x< x 0 тогда x < c < c 1 < x 0 и x – x 0 < 0, c – x 0 < 0, т.к. по условию то

Det er på samme måte bevist at hvis f¢¢(x) > 0 på intervallet (a, b), så er kurven y=f(x) konkav på intervallet (a, b).

Teoremet er bevist.

Definisjon. Punktet som skiller den konvekse delen av kurven fra den konkave delen kalles bøyningspunkt.

Tydeligvis skjærer tangenten kurven ved infleksjonspunktet.

Teorem 2. La kurven defineres av ligningen y = f(x). Hvis den andre deriverte f¢¢(a) = 0 eller f¢¢(a) ikke eksisterer og når den passerer gjennom punktet x = a f¢¢(x) skifter fortegn, vil punktet på kurven med abscissen x = a er et bøyningspunkt.

Bevis. 1) La f¢¢(x)< 0 при х < a и f¢¢(x) >0 for x > a. Så kl

x< a кривая выпукла, а при x >a kurven er konkav, dvs. punkt x = a – bøyningspunkt.

2) La f¢¢(x) > 0 for x< b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x >b – konveks oppover. Da er x = b bøyningspunktet.

Teoremet er bevist.

Asymptoter.

Når man studerer funksjoner, skjer det ofte at når x-koordinaten til et punkt på en kurve beveger seg til det uendelige, nærmer kurven seg på ubestemt tid en viss rett linje.

Definisjon. Den rette linjen kalles asymptote kurve hvis avstanden fra det variable punktet på kurven til denne rette linjen har en tendens til null når punktet beveger seg til uendelig.

Det skal bemerkes at ikke hver kurve har en asymptote. Asymptoter kan være rette eller skrå. Å studere funksjoner for tilstedeværelsen av asymptoter er av stor betydning og lar deg mer nøyaktig bestemme arten av funksjonen og oppførselen til kurvegrafen.

Generelt sett kan en kurve, som på ubestemt tid nærmer seg asymptoten, skjære den, og ikke på ett punkt, som vist i grafen til funksjonen nedenfor . Dens skrå asymptote er y = x.

La oss vurdere mer detaljert metodene for å finne asymptotene til kurver.

Vertikale asymptoter.

Fra definisjonen av en asymptote følger det at hvis eller eller , så er den rette linjen x = a asymptoten til kurven y = f(x).

For eksempel, for en funksjon, er linjen x = 5 en vertikal asymptote.

Skrå asymptoter.

Anta at kurven y = f(x) har en skrå asymptote y = kx + b.

La oss betegne skjæringspunktet for kurven og perpendikulæren til asymptoten - M, P - skjæringspunktet for denne perpendikulæren med asymptoten. La oss betegne vinkelen mellom asymptoten og okseaksen som j. Den vinkelrette MQ til okseaksen skjærer asymptoten i punkt N.

Da er MQ = y ordinaten til punktet på kurven, NQ = er ordinaten til punktet N på asymptoten.

I henhold til betingelsen: , ÐNMP = j, .

Vinkel j er konstant og ikke lik 90 0, da

Deretter .

Så den rette linjen y = kx + b er asymptoten til kurven. For nøyaktig å bestemme denne linjen, er det nødvendig å finne en måte å beregne koeffisientene k og b.

I det resulterende uttrykket tar vi x ut av parentes:

Fordi x®¥, da , fordi b = const, da .

Deretter , derfor,

.

Fordi , Det , derfor,

Merk at horisontale asymptoter er et spesialtilfelle av skrå asymptoter for k = 0.

Eksempel. .

1) Vertikale asymptoter: y®+¥ x®0-0: y®-¥ x®0+0, derfor er x = 0 en vertikal asymptote.

2) Skråasymptoter:

Dermed er den rette linjen y = x + 2 en skrå asymptote.

La oss plotte funksjonen:

Eksempel. Finn asymptoter og tegn grafen for funksjonen.

Linjene x = 3 og x = -3 er vertikale asymptoter av kurven.

La oss finne de skrå asymptotene:

y = 0 – horisontal asymptote.

Eksempel. Finn asymptoter og tegn grafen for funksjonen .

Den rette linjen x = -2 er den vertikale asymptoten til kurven.

La oss finne de skrå asymptotene.

Totalt sett er den rette linjen y = x – 4 en skrå asymptote.

Funksjonsstudieordning

Funksjonsforskningsprosessen består av flere stadier. For den mest komplette forståelsen av funksjonen til funksjonen og arten av dens graf, er det nødvendig å finne:

1) Funksjonens eksistensdomene.

Dette konseptet inkluderer både verdidomenet og definisjonsdomenet til en funksjon.

2) Brytepunkter. (Hvis tilgjengelig).

3) Intervaller for økning og reduksjon.

4) Maksimum og minimum poeng.

5) Maksimums- og minimumsverdien til en funksjon på dens definisjonsdomene.

6) Områder med konveksitet og konkavitet.

7) Bøyningspunkter (hvis noen).

8) Asymptoter (hvis noen).

9) Bygg en graf.

La oss se på anvendelsen av denne ordningen ved å bruke et eksempel.

Eksempel. Utforsk funksjonen og lag dens graf.

Vi finner funksjonens eksistensdomene. Det er åpenbart det definisjonsdomene funksjon er arealet (-¥; -1) È (-1; 1) È (1; ¥).

I sin tur er det klart at de rette linjene x = 1, x = -1 er vertikale asymptoter krokete.

Rekkevidde av verdier av denne funksjonen er intervallet (-¥; ¥).

Brytepunkter funksjoner er punkter x = 1, x = -1.

Vi finner kritiske punkter.

La oss finne den deriverte av funksjonen

Kritiske punkter: x = 0; x = - ; x = ; x = -1; x = 1.

La oss finne den andre deriverte av funksjonen

La oss bestemme konveksiteten og konkaviteten til kurven med intervaller.

-¥ < x < - , y¢¢ < 0, кривая выпуклая

- < x < -1, y¢¢ < 0, кривая выпуклая

1 < x < 0, y¢¢ >0, konkav kurve

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < , y¢¢ >0, konkav kurve

< x < ¥, y¢¢ >0, konkav kurve

Finne hullene økende Og synkende funksjoner. For å gjøre dette bestemmer vi tegnene til den deriverte av funksjonen på intervaller.

-¥ < x < - , y¢ >0, funksjonen øker

- < x < -1, y¢ < 0, функция убывает

1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢¢ >0, funksjonen øker

Det kan sees at punktet x = - er et punkt maksimum, og punkt x = er et punkt minimum. Funksjonsverdiene på disse punktene er lik henholdsvis -3 /2 og 3 /2.

Omtrent vertikalt asymptoter har allerede blitt sagt ovenfor. La oss nå finne skrå asymptoter.

Totalt er ligningen for den skrå asymptoten y = x.

La oss bygge rute Egenskaper:

Funksjoner av flere variabler

Når vi vurderer funksjoner til flere variabler, vil vi begrense oss til en detaljert beskrivelse av funksjonene til to variabler, siden alle oppnådde resultater vil være gyldige for funksjoner av et vilkårlig antall variabler.

Definisjon: Hvis hvert par av gjensidig uavhengige tall (x, y) fra et bestemt sett, ifølge en eller annen regel, er assosiert med en eller flere verdier av variabelen z, kalles variabelen z en funksjon av to variabler.

Definisjon: Hvis et tallpar (x, y) tilsvarer én verdi z, kalles funksjonen entydig, og hvis mer enn én, så – polysemantisk.

Definisjon: Definisjonsdomene funksjon z er settet med par (x, y) som funksjon z eksisterer for.

Definisjon: Nabolaget til et punkt M 0 (x 0, y 0) med radius r er settet av alle punkter (x, y) som tilfredsstiller betingelsen .

Definisjon: Tallet A kalles grense funksjon f(x, y) som punktet M(x, y) har en tendens til punktet M 0 (x 0, y 0), hvis det for hvert tall e > 0 er et tall r > 0 slik at for ethvert punkt M (x, y), som betingelsen er sann for

tilstanden er også sann .

Skrive ned:

Definisjon: La punktet M 0 (x 0, y 0) tilhøre definisjonsdomenet til funksjonen f(x, y). Da kalles funksjonen z = f(x, y). kontinuerlige ved punkt M 0 (x 0, y 0), if

(1)

og punktet M(x, y) tenderer til punktet M 0 (x 0, y 0) på en vilkårlig måte.

Hvis betingelsen (1) på noe tidspunkt ikke er oppfylt, kalles dette punktet bruddpunkt funksjoner f(x, y). Dette kan være i følgende tilfeller:

1) Funksjonen z = f(x, y) er ikke definert i punktet M 0 (x 0, y 0).

2) Det er ingen grense.

3) Denne grensen eksisterer, men den er ikke lik f(x 0 , y 0).

Eiendom. Hvis funksjonen f(x, y, …) er definert og kontinuerlig i en lukket og

avgrenset domene D, så er det i dette domenet minst ett punkt

N(x 0 , y 0 , …), slik at for de resterende punktene er ulikheten sann

f(x 0 , y 0 , …) ³ f(x, y, …)

samt punkt N 1 (x 01, y 01, ...), slik at for alle andre punkter er ulikheten sann

f(x 01 , y 01 , …) £ f(x, y, …)

så f(x 0 , y 0 , …) = M – høyeste verdi funksjoner, og f(x 01 , y 01 , ...) = m – minste verdi funksjoner f(x, y, …) i domene D.

En kontinuerlig funksjon i et lukket og avgrenset domene D når sin største verdi minst én gang og sin minste verdi én gang.

Eiendom. Hvis funksjonen f(x, y, …) er definert og kontinuerlig i et lukket avgrenset domene D, og ​​M og m er henholdsvis de største og minste verdiene av funksjonen i dette domenet, så for ethvert punkt m О det er et poeng

N 0 (x 0 , y 0 , …) slik at f(x 0 , y 0 , …) = m.

Enkelt sagt tar en kontinuerlig funksjon i domenet D alle mellomverdier mellom M og m. En konsekvens av denne egenskapen kan være konklusjonen at hvis tallene M og m har forskjellige fortegn, så forsvinner funksjonen i domenet D minst én gang.

Eiendom. Funksjon f(x, y, …), kontinuerlig i et lukket avgrenset domene D, begrenset i denne regionen, hvis det er et tall K slik at for alle punkter i regionen er ulikheten sann .

Eiendom. Hvis en funksjon f(x, y, …) er definert og kontinuerlig i et lukket avgrenset domene D, så jevnt kontinuerlig i dette området, dvs. for ethvert positivt tall e er det et tall D > 0 slik at for to punkter (x 1, y 1) og (x 2, y 2) i regionen som ligger i en avstand mindre enn D, gjelder ulikheten

De ovennevnte egenskapene ligner egenskapene til funksjoner til en variabel som er kontinuerlige i et intervall. Se Egenskaper for funksjoner kontinuerlig på et intervall.

Derivater og differensialer av funksjoner

flere variabler.

Definisjon. La funksjonen z = f(x, y) gis i et eller annet domene. La oss ta et vilkårlig punkt M(x, y) og sette inkrementet Dx til variabelen x. Da kalles mengden D x z = f(x + Dx, y) – f(x, y) delvis økning av funksjonen i x.

Du kan skrive ned

.

Da heter det delvis avledet funksjoner z = f(x, y) i x.

Betegnelse:

Den partielle deriverte av en funksjon med hensyn til y bestemmes på samme måte.

Geometrisk sans den partielle deriverte (la oss si) er tangenten til helningsvinkelen til tangenten trukket ved punktet N 0 (x 0, y 0, z 0) til seksjonen av overflaten av planet y = y 0.

Full inkrement og full differensial.

tangentplan

La N og N 0 være punkter på denne overflaten. La oss tegne en rett linje NN 0. Planet som går gjennom punktet N 0 kalles tangentplan til overflaten hvis vinkelen mellom sekanten NN 0 og dette planet tenderer mot null, når avstanden NN 0 har en tendens til null.

Definisjon. Normal til overflaten i punktet N 0 er en rett linje som går gjennom punktet N 0 vinkelrett på tangentplanet til denne overflaten.

På ethvert punkt har overflaten enten bare ett tangentplan eller har det ikke i det hele tatt.

Hvis overflaten er gitt ved likningen z = f(x, y), hvor f(x, y) er en funksjon som kan differensieres i punktet M 0 (x 0, y 0), vil tangentplanet i punktet N 0 ( x 0,y 0, ( x 0 ,y 0)) eksisterer og har ligningen:

Ligningen for normalen til overflaten på dette punktet er:

Geometrisk sans den totale differensialen til en funksjon av to variable f(x, y) i punktet (x 0, y 0) er økningen av applikatet (z-koordinatene) til tangentplanet til overflaten når man beveger seg fra punktet (x 0) , y 0) til punktet (x 0 + Dx, y 0 +Dу).

Som du kan se, er den geometriske betydningen av den totale differensialen til en funksjon av to variabler en romlig analog av den geometriske betydningen av differensialen til en funksjon av en variabel.

Eksempel. Finn likningene til tangentplanet og normalen til overflaten

ved punkt M(1, 1, 1).

Tangentplanligning:

Normal ligning:

Omtrentlig beregninger ved bruk av totale differensialer.

Den totale differensialen til funksjonen u er lik:

Den nøyaktige verdien av dette uttrykket er 1,049275225687319176.

Partielle derivater av høyere orden.

Hvis en funksjon f(x, y) er definert i et domene D, vil dens partielle derivater også bli definert i samme domene eller en del av det.

Vi vil kalle disse derivater første ordens partielle derivater.

Derivatene av disse funksjonene vil være andre ordens partielle derivater.

Ved å fortsette å differensiere de resulterende likhetene, oppnår vi partielle derivater av høyere orden.

1°

1°. Bestemmelse av ekstremumet til en funksjon.

Begrepene maksimum, minimum og ekstremum av en funksjon av to variabler ligner på de tilsvarende konseptene for en funksjon av en uavhengig variabel.

La funksjonen z =f (x ; y) definert på et eller annet område D punktum N (x 0;y 0) D.

Punktum (x 0;y 0) kalt et punkt maksimum funksjoner z= f (x ;y ), hvis det er et slikt -nabolag av punktet (x 0;y 0), det for hvert punkt (x;y), annerledes enn (x 0;y 0) fra dette nabolaget holder ulikheten f (x ;y)< f (x 0;y 0). I figur 12: N 1 - maksimum poeng, a N 2 - minimumspunktet for funksjonen z =f (x ;y).

Poenget bestemmes på samme måte minimum funksjoner: for alle punkter (x 0;y 0), annerledes enn (x 0;y 0), fra d -nabolaget til et punkt (x 0;y 0) ulikhet gjelder: f (x 0;y 0) >f (x 0;y 0).

Ytterpunktet til en funksjon av tre eller flere variabler bestemmes på samme måte.

Verdien av funksjonen ved maksimum (minimum) punkt kalles maksimum (minimum) funksjoner.

Maksimum og minimum av en funksjon kalles ytterpunkter.

Legg merke til at funksjonens ytterpunkt per definisjon ligger innenfor definisjonsdomenet til funksjonen; maksimum og minimum har lokale(lokalt) tegn: verdien av en funksjon i et punkt (x 0;y 0) sammenlignes med verdiene på punkter som er tilstrekkelig nærme (x 0;y 0). I området D en funksjon kan ha flere ytterpunkter eller ingen.

2°. Nødvendige forhold for et ekstremum.

La oss vurdere betingelsene for eksistensen av et ekstremum av en funksjon.

Geometriske likheter f"y (x 0;y 0)= 0 og f"y (x 0;y 0) = 0 betyr at ved funksjonens ytterpunkt z = f (x ; y) tangentplan til overflaten som representerer funksjonen f (x ; y), parallelt med flyet Å hehe fordi ligningen til tangentplanet er z =z 0.

Kommentar. En funksjon kan ha et ekstremum på punkter der minst en av de partielle deriverte ikke eksisterer. For eksempel funksjonen har et maksimum på punktet OM(0;0), men har ingen partielle derivater på dette tidspunktet.

Punktet der første ordens partielle deriverte av funksjonen z = f (x ;y) er lik null, dvs. f"x = 0, f" y= 0, ringte stasjonært punkt funksjoner z.

Stasjonære punkter og punkter der minst én partiell derivert ikke eksisterer kalles kritiske punkter.

På kritiske punkter kan funksjonen ha eller ikke ha et ekstremum. Likheten av partielle derivater til null er en nødvendig, men ikke tilstrekkelig betingelse for eksistensen av et ekstremum. Tenk for eksempel på funksjonen z = hu. For det er punktet 0(0; 0) kritisk (det blir null). Imidlertid er ekstremumfunksjonen i den z = xy ikke har, fordi i et tilstrekkelig lite nabolag til punktet O(0;0) er det punkter som z> 0 (poeng av 1. og 3. kvartal) og z< 0 (poeng av II og IV kvartaler).

For å finne ytterpunktene til en funksjon i et gitt område, er det derfor nødvendig å utsette hvert kritiske punkt i funksjonen for ytterligere forskning.

Stasjonære punkter finner man ved å løse ligningssystemet

fx (x, y) = 0, f"y (x, y) = 0

(nødvendige forhold for et ekstremum).

System (1) tilsvarer én ligning df(x, y)=0. Generelt, på ytterpunktet P(a, b) funksjoner f(x, y) eller df(x, y)=0, eller df(a, b) eksisterer ikke.

3°. Tilstrekkelige forhold for et ekstremum. La P(a; b)- stasjonært punkt for funksjonen f(x,y), dvs. . df(a, b) = 0. Deretter:

og hvis d2f (a, b)< 0 kl, da f(a, b) Det er maksimum funksjoner f (x, y);

b) hvis d2f (a, b) > 0 kl, da f(a, b)Det er minimum funksjoner f (x,y);

c) hvis d2f (a, b) endrer tegn, da f (a, b) er ikke et ekstremum av funksjonen f (x, y).

De gitte betingelsene tilsvarer følgende: la Og . La oss komponere diskriminerende Δ=AC -B².

1) hvis Δ > 0, så har funksjonen et ekstremum ved punktet P(a;b) nemlig maksimum if EN<0 (eller MED<0 ), og et minimum hvis A>0(eller С>0);

2) hvis Δ< 0, то экстремума в точке P(a; b) Nei;

3) hvis Δ =0, så spørsmålet om tilstedeværelsen av et ekstremum av funksjonen i punktet P(a; b) forblir åpen (mer forskning kreves).

4°. Tilfellet av en funksjon av flere variabler. For en funksjon av tre eller flere variabler, er de nødvendige betingelsene for eksistensen av et ekstremum lik betingelsene (1), og de tilstrekkelige forholdene ligner betingelsene a), b), c) 3°.

Eksempel. Undersøk ekstremumfunksjonen z=x³+3xy²-15x-12y.

Løsning. La oss finne partielle deriverte og lage et ligningssystem (1):

Ved å løse systemet får vi fire stasjonære punkter:

La oss finne 2. ordens deriverte

og skape en diskriminant Δ=AC - B² for hvert stasjonært punkt.

1) For punkt: , Δ=AC-B²=36-144<0 . Dette betyr at det ikke er noe ekstremum på punktet.

2) For punkt P2: A=12, B=6, C=12; Δ=144-36>0, A>0. Ved punkt P2 har funksjonen et minimum. Dette minimum er lik verdien av funksjonen ved x=2, y=1: ​​zmin=8+6-30-12=-28.

3) For punkt: A= -6, B=-12, C= -6; A = 36-144<0 . Det er ingen ekstrem.

4) For punkt P 4: A=-12, B=-6, C=-12; Δ=144-36>0. Ved punkt P4 har funksjonen et maksimum lik Zmax=-8-6+30+12=28.

5°. Betinget ekstremum. I det enkleste tilfellet betinget ekstremum funksjoner f(x,y) er maksimum eller minimum av denne funksjonen, oppnådd under forutsetning av at argumentene er relatert av ligningen φ(x,y)=0 (forbindelsesligning). For å finne det betingede ekstremumet til en funksjon f(x, y) i nærvær av en relasjon φ(x,y) = 0, utgjør den såkalte Lagrange funksjon

F (x,y )=f (x,y )+λφ (x,y ),

hvor λ er en udefinert konstant faktor, og det vanlige ytterpunktet for denne hjelpefunksjonen søkes. De nødvendige betingelsene for et ekstremum er redusert til et system med tre ligninger

med tre ukjente x, y, λ, hvorfra man generelt sett kan bestemme disse ukjente.

Spørsmålet om eksistensen og naturen til det betingede ekstremumet er løst basert på å studere tegnet til den andre differensialen til Lagrange-funksjonen

for verdisystemet som testes x, y, λ, hentet fra (2) forutsatt at dx Og dу knyttet til ligningen

.

Nemlig funksjonen f(x,y) har et betinget maksimum if d²F< 0, og et betinget minimum if d²F>0. Spesielt hvis diskriminanten Δ for funksjonen F(x,y) er positiv på et stasjonært punkt, så er det på dette punktet et betinget maksimum av funksjonen f(x, y), Hvis EN< 0 (eller MED< 0), og et betinget minimum if A > O(eller С>0).

Tilsvarende finnes det betingede ekstremumet til en funksjon av tre eller flere variabler i nærvær av en eller flere forbindelsesligninger (hvor antallet imidlertid må være mindre enn antallet variabler). Her må vi introdusere like mange usikre faktorer i Lagrange-funksjonen som det er koblingsligninger.

Eksempel. Finn ytterpunktet til funksjonen z = 6-4x -3y forutsatt at variablene X Og på tilfredsstille ligningen x²+y²=1.

Løsning. Geometrisk kommer problemet ned til å finne de største og minste verdiene av applikasjonen z flyet z=6 - 4x - Zu for skjæringspunktene mellom den og sylinderen x2+y2=1.

Kompilere Lagrange-funksjonen F(x,y)=6 -4x -3y+λ(x2+y2-1).

Vi har . De nødvendige forholdene gir ligningssystemet

løse som vi finner:

.

,

d²F = 2λ (dx²+dy²).

Hvis og, da d²F >0, og derfor har funksjonen på dette tidspunktet et betinget minimum. Hvis og så d²F<0, og derfor har funksjonen på dette tidspunktet et betinget maksimum.

Dermed,

6°. De største og minste verdiene til en funksjon.

La funksjonen z =f (x ; y) definert og kontinuerlig i et begrenset lukket område . Så når hun på noen punkter din største M og minst T verdier (såkalt globalt ekstremum). Disse verdiene oppnås av funksjonen på punkter som ligger inne i regionen , eller på punkter som ligger på grensen til regionen.

Ytterpunktet til en funksjon er punktet i definisjonsdomenet til funksjonen der verdien av funksjonen får en minimums- eller maksimumsverdi. Verdiene til funksjonen på disse punktene kalles ekstrema (minimum og maksimum) av funksjonen.

Definisjon. Punktum x1 funksjonsdomene f(x) er kalt maksimumspunktet for funksjonen , hvis verdien av funksjonen på dette punktet er større enn verdiene til funksjonen på punkter som er tilstrekkelig nærme den, plassert til høyre og venstre for den (det vil si at ulikheten gjelder f(x0 ) > f(x 0 + Δ x) x1 maksimum.

Definisjon. Punktum x2 funksjonsdomene f(x) er kalt minimumspunktet for funksjonen, hvis verdien av funksjonen på dette punktet er mindre enn verdiene til funksjonen ved punkter som er tilstrekkelig nærme den, plassert til høyre og venstre for den (det vil si at ulikheten gjelder f(x0 ) < f(x 0 + Δ x) ). I dette tilfellet sier vi at funksjonen har på punktet x2 minimum.

La oss si poeng x1 - maksimalt punkt for funksjonen f(x). Deretter i intervallet frem til x1 funksjonen øker, derfor er den deriverte av funksjonen større enn null ( f "(x) > 0 ), og i intervallet etter x1 funksjonen reduseres, derfor, avledet av en funksjon mindre enn null ( f "(x) < 0 ). Тогда в точке x1

La oss også anta at poenget x2 - minimumspunktet for funksjonen f(x). Deretter i intervallet frem til x2 funksjonen er avtagende, og den deriverte av funksjonen er mindre enn null ( f "(x) < 0 ), а в интервале после x2 funksjonen øker, og den deriverte av funksjonen er større enn null ( f "(x) > 0 ). I dette tilfellet også på punktet x2 den deriverte av funksjonen er null eller eksisterer ikke.

Fermats teorem (et nødvendig tegn på eksistensen av et ekstremum av en funksjon). Hvis poenget x0 - ekstremumpunktet for funksjonen f(x), så på dette tidspunktet er den deriverte av funksjonen lik null ( f "(x) = 0 ) eller eksisterer ikke.

Definisjon. Punktene der den deriverte av en funksjon er null eller ikke eksisterer kalles kritiske punkter .

Eksempel 1. La oss vurdere funksjonen.

På punktet x= 0 den deriverte av funksjonen er null, derfor punktet x= 0 er det kritiske punktet. Men som man kan se i grafen til funksjonen, øker den gjennom hele definisjonsdomenet, så poenget x= 0 er ikke ekstremumpunktet for denne funksjonen.

Dermed er betingelsene om at den deriverte av en funksjon i et punkt er lik null eller ikke eksisterer nødvendige betingelser for et ekstremum, men ikke tilstrekkelig, siden andre eksempler på funksjoner kan gis som disse betingelsene er oppfylt for, men funksjonen har ikke et ekstremum på det tilsvarende punktet. Derfor det må være tilstrekkelig bevis, slik at man kan bedømme om det er et ekstremum på et bestemt kritisk punkt og hva slags ekstremum det er - maksimum eller minimum.

Teorem (det første tilstrekkelige tegnet på eksistensen av et ekstremum av en funksjon). Kritisk punkt x0 f(x) hvis, når den passerer gjennom dette punktet, den deriverte av funksjonen endrer fortegn, og hvis tegnet endres fra "pluss" til "minus", så er det et maksimumspunkt, og hvis fra "minus" til "pluss", så det er et minimumspoeng.

Hvis nærme punktet x0 , til venstre og til høyre for den, beholder den deriverte tegnet sitt, dette betyr at funksjonen enten bare reduseres eller bare øker i et bestemt nabolag av punktet x0 . I dette tilfellet, på punktet x0 det er ingen ekstrem.

Så, for å bestemme ekstremumpunktene til funksjonen, må du gjøre følgende :

1. Finn den deriverte av funksjonen.
2. Lik den deriverte til null og bestem de kritiske punktene.
3. Mentalt eller på papir, merk de kritiske punktene på talllinjen og bestem tegnene til den deriverte av funksjonen i de resulterende intervallene. Hvis tegnet på den deriverte endres fra "pluss" til "minus", er det kritiske punktet maksimumspunktet, og hvis fra "minus" til "pluss", så er minimumspunktet.
4. Regn ut verdien av funksjonen ved ytterpunktene.

Eksempel 2. Finn ytterpunktene til funksjonen .

Løsning. La oss finne den deriverte av funksjonen:

La oss likestille den deriverte til null for å finne de kritiske punktene:

.

Siden for noen verdier av "x" er nevneren ikke lik null, likestiller vi telleren til null:

Har ett kritisk poeng x= 3. La oss bestemme tegnet til den deriverte i intervallene avgrenset av dette punktet:

i intervallet fra minus uendelig til 3 - et minustegn, det vil si at funksjonen reduseres,

i intervallet fra 3 til pluss uendelig er det et plusstegn, det vil si at funksjonen øker.

Det vil si punktum x= 3 er minimumspunktet.

La oss finne verdien av funksjonen ved minimumspunktet:

Dermed finnes funksjonens ekstremumpunkt: (3; 0), og det er minimumspunktet.

Teorem (det andre tilstrekkelige tegnet på eksistensen av et ekstremum av en funksjon). Kritisk punkt x0 er funksjonens ytterpunkt f(x) hvis den andre deriverte av funksjonen på dette tidspunktet ikke er lik null ( f ""(x) ≠ 0 ), og hvis den andre deriverte er større enn null ( f ""(x) > 0 ), så maksimumspunktet, og hvis den andre deriverte er mindre enn null ( f ""(x) < 0 ), то точкой минимума.

Merknad 1. Hvis på punktet x0 Hvis både den første og andre deriverte forsvinner, er det på dette tidspunktet umulig å bedømme tilstedeværelsen av et ekstremum basert på det andre tilstrekkelige kriteriet. I dette tilfellet må du bruke det første tilstrekkelige kriteriet for ytterpunktet til en funksjon.

Merknad 2. Det andre tilstrekkelige kriteriet for ekstremumet til en funksjon er ikke anvendelig selv når den første deriverte ikke eksisterer på et stasjonært punkt (da eksisterer heller ikke den andre deriverte). I dette tilfellet må du også bruke det første tilstrekkelige tegnet på et ekstremum av en funksjon.

Lokal karakter av ytterpunktene av funksjonen

Av definisjonene ovenfor følger det at ytterpunktet til en funksjon er lokalt av natur - det er den største og minste verdien av funksjonen sammenlignet med nærliggende verdier.

La oss si at du ser på inntektene dine over en periode på ett år. Hvis du i mai tjente 45 000 rubler, og i april 42 000 rubler og i juni 39 000 rubler, er inntektene i mai det maksimale av inntektsfunksjonen sammenlignet med nærliggende verdier. Men i oktober tjente du 71 000 rubler, i september 75 000 rubler og i november 74 000 rubler, så oktoberinntektene er minimumsinntektsfunksjonen sammenlignet med nærliggende verdier. Og du kan enkelt se at maksimum blant verdiene april-mai-juni er mindre enn minimum september-oktober-november.

Generelt sett kan en funksjon på et intervall ha flere ekstrema, og det kan vise seg at et minimum av funksjonen er større enn et maksimum. Så, for funksjonen vist i figuren ovenfor, .

Det vil si at man ikke skal tro at maksimum og minimum av en funksjon er henholdsvis dens største og minste verdi på hele segmentet som vurderes. På maksimumspunktet har funksjonen den største verdien bare sammenlignet med de verdiene som den har på alle punkter tilstrekkelig nær maksimumspunktet, og ved minimumspunktet har den den minste verdien bare i sammenligning med disse verdiene at den på alle punkter er tilstrekkelig nær minimumspunktet.

Derfor kan vi klargjøre konseptet ovenfor med ekstremumpunkter for en funksjon og kalle minimumspoeng lokale minimumspunkter, og maksimumspoeng lokale maksimumspoeng.

Vi ser etter funksjonens ytterpunkt sammen

Eksempel 3.

Løsning: Funksjonen er definert og kontinuerlig på hele tallinjen. Dens derivat finnes også på hele tallinjen. Derfor, i dette tilfellet, er de kritiske punktene bare de der, dvs. , hvorfra og . Kritiske poeng og del opp hele definisjonsdomenet av funksjonen i tre intervaller for monotonisitet: . La oss velge ett kontrollpunkt i hver av dem og finne tegnet til den deriverte på dette punktet.

For intervallet kan kontrollpunktet være: finn. Å ta et poeng i intervallet, får vi, og å ta et poeng i intervallet har vi. Så, i intervallene og , og i intervallet . I henhold til det første tilstrekkelige kriteriet for et ekstremum er det ikke noe ekstremum i punktet (siden den deriverte beholder fortegnet i intervallet), og ved punktet har funksjonen et minimum (siden den deriverte skifter fortegn fra minus til pluss ved passering gjennom dette punktet). La oss finne de tilsvarende verdiene til funksjonen: , a . I intervallet reduseres funksjonen, siden i dette intervallet , og i intervallet øker den, siden i dette intervallet .

For å tydeliggjøre konstruksjonen av grafen finner vi skjæringspunktene til den med koordinataksene. Når vi får en ligning hvis røtter er og , dvs. to punkter (0; 0) og (4; 0) av grafen til funksjonen blir funnet. Ved å bruke all informasjonen som er mottatt, bygger vi en graf (se begynnelsen av eksemplet).

For egenkontroll under beregninger kan du bruke online derivatkalkulator .

Eksempel 4. Finn ytterpunktene til funksjonen og bygg dens graf.

Definisjonsdomenet til en funksjon er hele tallinjen, bortsett fra punktet, dvs. .

For å forkorte studiet kan du bruke det faktum at denne funksjonen er jevn, siden . Derfor er grafen symmetrisk om aksen Oy og studien kan kun utføres i intervallet.

Å finne den deriverte og kritiske punkter ved funksjonen:

1) ;

2) ,

men funksjonen lider av en diskontinuitet på dette punktet, så det kan ikke være et ekstremumpunkt.

Dermed har den gitte funksjonen to kritiske punkter: og . Tar vi hensyn til funksjonens paritet, vil vi bare sjekke punktet ved å bruke det andre tilstrekkelige kriteriet for et ekstremum. For å gjøre dette finner vi den andre deriverte og bestemme dets fortegn ved: vi får . Siden og , er det minimumspunktet for funksjonen, og .

For å få et mer fullstendig bilde av grafen til en funksjon, la oss finne ut dens oppførsel ved grensene til definisjonsdomenet:

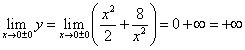
(her indikerer symbolet ønsket x til null fra høyre, og x forblir positiv; betyr på samme måte aspirasjon x til null fra venstre, og x forblir negativ). Så hvis , så . Deretter finner vi

,

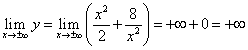de. hvis da .

Grafen til en funksjon har ingen skjæringspunkter med aksene. Bildet er i begynnelsen av eksemplet.

For egenkontroll under beregninger kan du bruke online derivatkalkulator .

Vi fortsetter å søke etter ekstrema av funksjonen sammen

Eksempel 8. Finn ytterpunktene til funksjonen.

Løsning. La oss finne definisjonsdomenet til funksjonen. Siden ulikheten må tilfredsstilles, henter vi fra .

La oss finne den første deriverte av funksjonen.